Primarstufe

Du magst Rätsel und möchtest gerne programmieren lernen? Dann bist du hier genau richtig!

In den nächsten Wochen tauchen wir gemeinsam in die Welt des Programmierens ein. Jede Woche behandeln wir ein neues Thema und stellen dir knifflige Aufgaben. Es gibt jeweils mehrere Knobelaufgaben von unterschiedlicher Schwierigkeit. Du kannst auswählen, welche du lösen möchtest.

Was ist Logo?

Logo ist eine Programmiersprache für Kinder. Im Zentrum steht eine Schildkröte, die auf Befehl bunte Muster auf den Bildschirm malt. Keine Angst, das ist nicht schwer! Die Schildkröte versteht nämlich nur sehr wenige Wörter oder Befehle. In ein paar Wochen könnt ihr euch fliessend verständigen und immer schönere und komplexere Bilder zeichnen.

Kalenderwoche 14/15

Diese Challenge läuft von Mittwoch, dem 1. April 2020, bis Dienstag, dem 7. April 2020. Am Mittwoch, dem 8. April 2020, laden wir einen Lösungsvorschlag hoch.

Tutorial

Wir verwenden die Programmierumgebung XLogoOnline (opens new window) und zeigen dir im folgenden Tutorial wie man damit programmieren kann:

Unser Übungsheft mit etlichen Übungsaufgaben findest du hier (opens new window). Das Thema dieser Woche lautet Grundbefehle (Kapitel 1).

Befehlsübersicht

Logo umfasst genau fünf Befehle, die es erlauben, die Schildkröte zu steuern.

Die Schildkröte kann...

Befehl	Beschreibung
fd 100	eine gewisse Distanz (z.B. 100 Schritte) vorwärts gehen.
bk 100	eine gewisse Distanz (z.B. 100 Schritte) rückwärts gehen.
rt 90	sich um einen gewissen Winkel (z.B. 90 Grad) nach rechts drehen.
lt 90	sich um einen gewissen Winkel (z.B. 90 Grad) nach links drehen.
cs	die Zeichnung löschen und wieder zur Mitte des Bildschirms zurückkehren.

Die Befehle führen zu folgenden Aktionen der Schildkröte:

Achtung: Bei Tippfehlern und fehlenden Abständen. Fehler sind einfach zu erkennen, denn sie werden rot unterstrichen.

Aus mehreren Befehlen können sogenannte Programme gebildet werden. Diese bestehen aus mehreren aneinandergereihten Befehlen. Probier's aus.

Challenge

Lösung anzeigen

Challenge 1

Die Schwierigkeit dieser Aufgabe besteht darin, dass bei gewissen Strecken nicht bekannt ist, wie lang diese sind. Besonders knifflig sind zwei Angaben: (a) die Höhe der Burg vom Boden bis zum oberen Ende der ersten Zinne und (b) die Breite des Tors. Um diese Angaben herauszufinden, müssen wir die Grössenverhältnisse der Burg studieren.

Zunächst fällt auf, dass alle Zinnen gleich hoch und breit sind, nämlich genau 100 Schritte. Aus dieser Erkenntnis lässt sich die Breite des Tors ablesen, dieses ist 300 Schritte breit, wie im nächsten Bild unten dargestellt.

Auch die Höhe der Burg lässt sich ganz ähnlich berechnen. Wir wissen, dass sich diese zusammensetzt aus der Höhe des Tors (400 Schritte), sowie der Höhe einer Zinne (100 Schritte) und dem Zwischenbereich zwischen Tor und Zinne (100 Schritte). Somit folgt, dass die Burg 600 Schritte hoch sein muss.

Daraus erschliessen wir sämtliche Seitenlängen der Burg:

Wir verbinden all diese Erkenntnisse und schreiben daraus das folgende Programm:

Hinweis: Hier gibt es verschiedene Lösungen.

fd 600 rt 90 
fd 100 rt 90 fd 100 lt 90 fd 100 lt 90 fd 100 rt 90 
fd 100 rt 90 fd 100 lt 90 fd 100 lt 90 fd 100 rt 90 
fd 100 rt 90 
fd 600 rt 90 
fd 500 bk 100 rt 90 
fd 400 rt 90 fd 300 rt 90 fd 400

Challenge 2

Zunächst überlegen wir uns, wie die Lösung aussehen könnte, wenn das Kreuz nicht gedreht wäre, sondern gerade stehen würde wie links im Bild dargestellt:

In diesem Fall ist eine Lösung schnell gefunden; beispielsweise so:

fd 400 rt 90 fd 100 rt 90 fd 400 lt 90 
fd 400 rt 90 fd 100 rt 90 fd 400 lt 90 
fd 400 rt 90 fd 100 rt 90 fd 400 lt 90 
fd 400 rt 90 fd 100 rt 90 fd 400 lt 90

Nun stellt sich jedoch die Frage, wie man das Kreuz noch rotieren kann. Dazu beobachten wir die Ausrichtung der Schildkröte auf dem Bild. Bevor wir anfangen, zu zeichnen, versuchen wir die Schildkröte so auszurichten, wie es rechts im Bild dargestellt ist.

Bei genauer Betrachtung der Skizze stellen wir fest, dass die Schildkröte im rechten Bild um 45° nach rechts gedreht ist, wenn man sie mit der Schildkröte im linken Bild vergleicht. Es genügt also, die Schildkröte am Anfang des Programms um 45° zu drehen, anschliessend zeichnet sie das Kreuz genau so wie wir es im ersten Programm gemacht haben:

rt 45
fd 400 rt 90 fd 100 rt 90 fd 400 lt 90 
fd 400 rt 90 fd 100 rt 90 fd 400 lt 90 
fd 400 rt 90 fd 100 rt 90 fd 400 lt 90 
fd 400 rt 90 fd 100 rt 90 fd 400 lt 90

Challenge 3

Wir lösen das Problem in fünf Schritten.

1. Zunächst zeichnen wir mit der Schildkröte ein Rechteck der Grösse 150 x 400:

fd 150 rt 90 fd 400 rt 90 
fd 150 rt 90 fd 400 rt 90

2. Danach suchen wir nach dem grösstmöglichen Quadrat, das wir über das Rechteck legen können. Unser Ziel ist es, ein Quadrat zu finden, das so gross wie möglich ist, aber dennoch nicht über die Grenzen des Rechtecks hinausragt. In einem Rechteck der Grösse 150 x 400 ist ein solches Quadrat eines der Grösse 150 x 150 Schildkrötenschritte.

fd 150 rt 90 fd 400 rt 90 
fd 150 rt 90 fd 400 rt 90

fd 150 rt 90 
fd 150 rt 90
fd 150 rt 90
fd 150 rt 90 

3. Als Nächstes versuchen wir, so viele solche Quadrate wie möglich nebeneinander zupacken, ohne dass sich diese überlappen. Um die Übrigbleibsel kümmern wir uns danach...

fd 150 rt 90 fd 400 rt 90 
fd 150 rt 90 fd 400 rt 90

fd 150 rt 90 
fd 150 rt 90 
fd 150 rt 90
fd 150 rt 90

rt 90 fd 150 lt 90 

fd 150 rt 90 
fd 150 rt 90 
fd 150 rt 90
fd 150 rt 90

4. Nach zwei Quadraten der Grösse 150 x 150 sind wir nicht mehr in der Lage, noch ein drittes derartiges Quadrat zu zeichnen, denn dazu bleibt nicht genügend Platz. Also suchen wir das nächstkleinere Quadrat, das möglichst viel der Fläche füllt – clever! 😃

Es handelt sich dabei um ein Quadrat der Grösse 100 x 100.

fd 150 rt 90 fd 400 rt 90 
fd 150 rt 90 fd 400 rt 90

fd 150 rt 90 
fd 150 rt 90 
fd 150 rt 90
fd 150 rt 90

rt 90 fd 150 lt 90 

fd 150 rt 90 
fd 150 rt 90 
fd 150 rt 90
fd 150 rt 90

rt 90 fd 150 lt 90

fd 100 rt 90
fd 100 rt 90
fd 100 rt 90
fd 100 rt 90

5. Der Platz reicht für ein zweites Quadrat der Grösse 100 x 100 nicht aus, also suchen wir nach dem nächstkleineren Quadrat, das möglichst viel der verbleibenden Fläche füllt. Es handelt sich dabei um ein Quadrat der Grösse 50 x 50 – und wir schaffen es, zwei davon nebeneinander zu packen.

Die fertige Lösung des Problems sieht wie folgt aus:

fd 150 rt 90 fd 400 rt 90 
fd 150 rt 90 fd 400 rt 90

fd 150 rt 90 
fd 150 rt 90 
fd 150 rt 90
fd 150 rt 90

rt 90 fd 150 lt 90 

fd 150 rt 90 
fd 150 rt 90 
fd 150 rt 90
fd 150 rt 90

rt 90 fd 150 lt 90

fd 100 rt 90
fd 100 rt 90
fd 100 rt 90
fd 100 rt 90

fd 100

fd 50 rt 90
fd 50 rt 90
fd 50 rt 90
fd 50 rt 90

rt 90 fd 50 lt 90

fd 50 rt 90
fd 50 rt 90
fd 50 rt 90
fd 50 rt 90

Kalenderwoche 15/16

Diese Challenge läuft von Mittwoch, dem 8. April 2020, bis Dienstag, dem 14. April 2020. Am Mittwoch, dem 15. April 2020, laden wir einen Lösungsvorschlag hoch.

Tutorial

Diese Woche lernen wir zwei neue Befehle kennen. Einerseits den Befehl setpc, mit welchem sich die Stiftfarbe ändern lässt, andererseits den Befehl repeat, mit welchem sich wiederholende Muster kurz und einfach beschreiben lassen.

Wir verwenden weiterhin die Programmierumgebung XLogoOnline (opens new window) und bearbeiten nun im Übungsheft (opens new window) die Aufgaben 6-14 (Kapitel 2, Der Befehl repeat).

Befehlsübersicht

Neben den fünf Befehlen fd, bk, rt, lt und cs verwenden wir diese Woche zwei neue Befehle, nämlich:

Befehl	Beschreibung
setpc farbe	Setze die Stiftfarbe. Ab diesem Moment werden sämtliche zukünftigen Linien in der angegebenen Farbe gezeichnet, bis die Stiftfarbe erneut gewechselt wird. Es stehen mehrere Farben zur Auswahl: green, blue, yellow, orange, brown, white, …
repeat zahl [befehle]	Der Befehle repeat erlaubt es, eine Folge von Befehlen wiederholt auszuführen. Ein Beispiel: repeat 4 [fd 100 rt 90] wiederholt die beiden Befehle fd 100 rt 90 insgesamt 4 Mal. Der Befehl repeat bietet also eine Kurzform für: fd 100 rt 90 fd 100 rt 90 fd 100 rt 90 fd 100 rt 90

Challenge

Auch diese Woche haben wir drei Knobelaufgaben für dich vorbereitet:

Eine kleine Aufgabe für die Ferien

Tobe dich aus – zeichne mit der Schildkröte dein Osterparadies und schick uns dein Bild per E-Mail an weekly-challenge (at) inf.ethz.ch.

Lösung anzeigen

Challenge 1

In dieser Aufgabe müssen wir den frisch gelernten Befehl septc einsetzen – und dies obwohl das Bild alles andere als farbig ist! Glaubst du nicht? Dann lies weiter... 😉

Wir gehen eine mögliche Lösung gemeinsam durch und betrachten dazu drei Schritte:

• 1. Schritt

Zunächst überlegen wir uns, an welcher Stelle wir das Muster beginnen wollen. Wir entscheiden uns hier, unten links zu beginnen (es wären jedoch auch andere Startpositionen möglich):

• 2. Schritt

Wir stellen fest, dass es sich bei dieser Figur um ein Quadrat der Seitenlänge 300 handelt. Jede Seite besteht aus zwei schwarzen und einer weissen Teilstrecke. Alle drei Teilstrecken sind jeweils gleich lang. Die Seite misst insgesamt eine Länge von 300 Schritten und somit muss also jede der drei Teilstrecken genau 100 Schritte lang sein.

Wir schreiben das Programm für alle 4 Seiten aus und verwenden den Befehl setpc um die Stiftfarbe jeweils zwischen schwarz und weiss zu tauschen:

fd 100 setpc white fd 100 setpc black fd 100 rt 90
fd 100 setpc white fd 100 setpc black fd 100 rt 90
fd 100 setpc white fd 100 setpc black fd 100 rt 90
fd 100 setpc white fd 100 setpc black fd 100 rt 90

• Schritt 3:

Das Programm funktioniert, ist allerdings noch unnötig lang. Um es zu kürzen, verwenden wir den Befehl repeat und stellen uns zu diesem Zweck zwei Fragen:

1. Welches Muster wiederholt sich in unserem Programm?
2. Wie oft wird dieses Muster wiederholt?

Bei genauerer Betrachtung unserer Lösung in Schritt 2 fällt auf, dass wir vier Mal dieselben Programmzeilen geschrieben haben. Jede Zeile entspricht einer Seite des Quadrats. Mit dieser Erkenntnis können wir das Programm nun kürzen, indem wir den Befehl repeat verwenden:

repeat 4 [fd 100 setpc white fd 100 setpc black fd 100 rt 90]

Aufgepasst:

Wenn wir ein Programm zu einer Seite des Quadrats schreiben, müssen wir uns jeweils auch Gedanken darüber machen, in welche Richtung die Schildkröte schaut, wenn sie eine Seite beginnt beziehungsweise beendet. Der Befehl rt 90 am Ende unseres Programmes hat dafür gesorgt, dass unsere Schildkröte jeweils richtig positioniert war, um die nächste Seite des Quadrats zu beginnen.

Challenge 2

Wir entscheiden uns zunächst für einen geeigneten Startpunkt und wählen hier die linke untere Ecke des ersten Quadrats. Die Lösung wird nun in drei Schritten präsentiert:

• Schritt 1:

Wir schreiben ein Programm, um das erste Quadrat zu zeichnen. Wir setzen die Stiftfarbe auf orange und beginnen anschliessend damit, das Quadrat zu zeichnen.

setpc orange fd 100 rt 90 fd 100 rt 90 fd 100 rt 90 fd 100

Nachdem wir das Programm ausgeführt haben, befindet sich die Schildkröte wieder in der linken unteren Ecke wie hier abgebildet:

• Schritt 2:

Nun geht es darum, die Schildkröte für das zweite Quadrat richtig zu positionieren. Der Startpunkt des zweiten Quadrats (also dessen linke untere Ecke) liegt in der Mitte der rechten Seite des bereits gezeichneten Quadrats. Um diesen Punkt zu erreichen, schreiben wir das folgende Programm:

bk 100 rt 90 fd 50

Die Schildkröte befindet sich nun an der richtigen Stelle, um jetzt das zweite und alle weiteren Quadrate zu zeichnen:

• Schritt 3:

Mit den zwei bisherigen Programmteilen, können wir das gesamte Muster zeichnen, indem wir fünf Mal das Grundmuster (also das Quadrat) sowie fünf Mal die Ausrichtung ausführen:

setpc orange fd 100 rt 90 fd 100 rt 90 fd 100 rt 90 fd 100
bk 100 rt 90 fd 50
setpc orange fd 100 rt 90 fd 100 rt 90 fd 100 rt 90 fd 100
bk 100 rt 90 fd 50
setpc orange fd 100 rt 90 fd 100 rt 90 fd 100 rt 90 fd 100
bk 100 rt 90 fd 50
setpc orange fd 100 rt 90 fd 100 rt 90 fd 100 rt 90 fd 100
bk 100 rt 90 fd 50
setpc orange fd 100 rt 90 fd 100 rt 90 fd 100 rt 90 fd 100
bk 100 rt 90 fd 50

Wir erhalten zwar das erwünschte Resultat...

• Schritt 4:

... allerdings benötigen wir dazu sage und schreibe 44 Befehle. Wie gelingt es uns, die fünf Quadrate mit weniger als 15 Befehlen zu zeichen?

Kein Problem! Wir setzen dazu den Befehl repeat ein, um die unnötigen Wiederholungen zu vermeiden. Betrachten wir die Lösung aus Schritt 3, so fällt nämlich schnell auf, dass wir dieselben zwei Zeilen immer wieder wiederholen:

setpc orange fd 100 rt 90 fd 100 rt 90 fd 100 rt 90 fd 100
bk 100 rt 90 fd 50

Wir fassen die beiden Zeilen also zusammen und wiederholen diese 5 Mal, um am Schluss die fünf Quadrate zu zeichnen:

repeat 5 [setpc orange fd 100 rt 90 fd 100 rt 90 fd 100 rt 90 fd 100 bk 100 rt 90 fd 50]

Diese Lösung erfordert nur noch 12 Befehle und genügt somit der Aufgabenstellung.

Aufgepasst:

• Zur Ausrichtung in Schritt 2 gibt es mehrere Möglichkeiten: Eine im Uhrzeigersinn und eine gegen den Uhrzeigersinn. Wir haben hier die Lösung im Gegenuhrzeigersinn gewählt, da sie das kürzere Resultat ergibt. Auch der andere Weg würde jedoch zu einer Lösung mit weniger als 15 Befehlen führen (nämlich genau 14).
• Findest du es auch unnötig, die Stiftfarbe fünf Mal auf orange zu setzen? Du kannst das Problem beheben, indem du setpc orange nur einmal ausführst bevor der repeat-Befehl beginnt:

setpc orange 
repeat 5 [fd 100 rt 90 fd 100 rt 90 fd 100 rt 90 fd 100 bk 100 rt 90 fd 50]

Challenge 3

Hierbei handelt es sich um eine knifflige Aufgabe, die jedoch einfach beginnt... Wir lösen sie in fünf Schritten:

• Schritt 1:

Wir beginnen mit dem Stamm der Palme und bereiten die Schildkröte darauf vor, anschliessend das erste grüne Blatt links zu zeichnen.

setpc brown 
fd 400
lt 90
setpc green

• Schritt 2:

Um nun das erste Blatt zu zeichnen, bewegen wir die Schildkröte 200 Schritte vorwärts und wieder zurück:

fd 200 bk 200

Die Schildkröte befindet sich wieder da, wo sie zuvor war, hat nun jedoch das erste Blatt gezeichnet:

• Schritt 3:

Um das zweite Blatt zu zeichnen, müssen wir bestimmen, um wie viel Grad sich die Schildkröte drehen muss, bevor sie mit dem nächsten Blatt beginnt.

Wenn wir das Bild genau betrachten, stellen wir fest, dass die Schildkröte am Schluss (nachdem sie 11 Blätter gezeichnet hat) in die entgegengesetzte Richtung schaut – sie dreht sich also während des Zeichnens der Blätter insgesamt um 180 Grad. Diese Drehung wird aufgeteilt auf 10 indentische Teilstücke (Hinweis: Es sind zwar 11 Blätter, aber nur 10 Winkel zwischen diesen Blättern! Zähle sie!). 180 Grad aufgeteilt auf 10 Teile ergibt 18 Grad pro Zwischenwinkel. Das benutzen wir, um das Blätterdach zu zeichnen:

fd 200 bk 200
rt 18
fd 200 bk 200
rt 18
fd 200 bk 200
rt 18
fd 200 bk 200
rt 18
fd 200 bk 200
rt 18
fd 200 bk 200
rt 18
fd 200 bk 200
rt 18
fd 200 bk 200
rt 18
fd 200 bk 200
rt 18
fd 200 bk 200
rt 18
fd 200 bk 200
rt 18

Was uns das erwünschte Resultat zeigt:

• Schritt 4:

Das Programm ist nun zwar korrekt, aber es ist noch immer unnötig lang. Wir können das Programm kürzer fassen, indem wir den Befehl repeat verwenden, denn in der Lösung in Schritt 3 erkennen wir klar ein sich wiederholendes Muster. Wir sehen elf Mal dieselben zwei Zeilen:

fd 200 bk 200
rt 18

Wir kürzen das Programm mit dem Befehl repeat...

repeat 11 [fd 200 bk 200 rt 18]

• Schritt 5:

... und verbinden zum Schluss alle Teile zur folgenden Lösung:

setpc brown  
fd 400 
lt 90 
setpc green
repeat 11 [fd 200 bk 200 rt 18]

Beiträge von euch

Hier präsentieren wir ein paar ausgewählte Beiträge, die uns per E-Mail erreicht haben:

Vielen Dank für eure Teilnahme und das Einsenden eurer tollen Lösungen!

Kalenderwoche 16/17

Diese Challenge läuft von Mittwoch, dem 15. April 2020, bis Dienstag, dem 21. April 2020. Am Mittwoch, dem 22. April 2020, laden wir einen Lösungsvorschlag hoch.

Tutorial

Diese Woche vertiefen wir das Thema Repetition mittels repeat und führen zudem zwei neue Befehle ein. Es handelt sich dabei um die Befehle pu und pd, mit welchen sich der Stift von der Zeichenfläche abheben respektive wieder absetzen lässt.

Wir verwenden weiterhin die Programmierumgebung XLogoOnline (opens new window) und bearbeiten nun im Übungsheft (opens new window) die Aufgaben 15-16 (Kapitel 2, Der Wandermodus).

Befehlsübersicht

Wir verwenden ausserdem neben den bereits bekannten Befehlen zwei weitere Befehle, nämlich pu (kurz für penup) sowie pd (kurz für pendown) :

Befehl	Beschreibung
pu	Der Befehl pu startet den Wandermodus. Die Schildkröte hebt dabei den Stift von der Zeichenfläche ab und bewegt sich ab diesem Moment ohne eine Spur zu hinterlassen.
pd	Der Befehl pd beendet den Wandermodus. Die Schildkröte senkt also den Stift wieder ab und hinterlässt ab diesem Moment wieder eine Spur, wenn sie sich bewegt.

Challenge

Auch diese Woche haben wir drei Knobelaufgaben für dich vorbereitet:

Eine kleine Aufgabe für die Ferien

Tobe dich aus – zeichne mit der Schildkröte dein Traumhaus und verwende dabei mindestens drei Mal den Befehl penup. Schick uns dein Bild per E-Mail an weekly-challenge (at) inf.ethz.ch.

Lösung anzeigen

Challenge 1

Beim Zeichnen von diesen bunten Quadraten musstest du auf zwei Dinge achten:

1. Du solltest die Befehle pu, pd und repeat einsetzen
2. Du solltest ein möglichst kurzes Programm dazu schreiben!

Wir gehen nun gemeinsam eine mögliche Lösung durch und betrachten dazu 4 Schritte:

• Schritt 1:

Wir beginnen mit dem ersten Quadrat links in der Abbildung. Wie immer, überlegen wir uns zunächst, an welcher Stelle wir unser Quadrat beginnen wollen. Wir entscheiden uns dafür, unten links zu beginnen. (Wie immer, wären auch andere Startpositionen möglich).

Aufgepasst: Für das Zeichnen eines Quadrats müssen wir auf die Farben achten.

setpc red fd 100 rt 90 
setpc yellow fd 100 rt 90 
setpc red fd 100 rt 90 
setpc yellow fd 100

Nachdem wir das Programm ausgeführt haben, befindet sich die Schildkröte wieder in der linken unteren Ecke wie hier abgebildet. Dabei ist sie nach links gedreht, da wir am Schluss des obigen Programms den Befehl rt 90 nicht eingesetzt haben.

• Schritt 2:

Nun geht es darum, die Schildkröte für das zweite Quadrat richtig zu positionieren. Der Startpunkt des zweiten Quadrats (also dessen linke untere Ecke) liegt rechts neben dem ersten Quadrat.

Wir kennen die Seitenlängen des Quadrats und auch die Länge der Strecke zwischen den beiden Quadraten. Nun geht es darum, den Punkt zu erreichen, wo unsere Schildkröte mit dem Zeichnen des nächsten Quadrates beginnen kann:

Aufgepasst: Weil die Schildkröte beim Zeichnen des ersten Quadrats nach oben geschaut hat, soll es auch bei den weiteren Quadraten so sein! Noch einen weiteren Tipp: Mit dem Befehl pu bewegst du die Schildkröte ohne eine Spur zu hinterlassen. Damit sie jedoch das nächste Quadrat zeichnen kann, muss der Stift wieder am Boden liegen. Dies erreichst du, in dem zu den Befehl pd verwendest bevor du das zweite Quadrat zeichnest.

pu bk 200 rt 90 pd

Die Schildkröte befindet sich nun an der richtigen Stelle, um jetzt das zweite und auch das dritte Quadrat zu zeichnen:

• Schritt 3:

Mit den bisherigen Programmteilen, können wir die drei Quadrate zeichnen, indem wir 3 Mal das Quadrat sowie 3 Mal die Ausrichtung ausführen:

setpc red fd 100 rt 90 setpc yellow fd 100 rt 90 setpc red fd 100 rt 90 setpc yellow fd 100
pu bk 200 rt 90 pd

setpc red fd 100 rt 90 setpc yellow fd 100 rt 90 setpc red fd 100 rt 90 setpc yellow fd 100
pu bk 200 rt 90 pd

setpc red fd 100 rt 90 setpc yellow fd 100 rt 90 setpc red fd 100 rt 90 setpc yellow fd 100
pu bk 200 rt 90 pd

Tatsächlich erhalten wir das gewünschte Bild…

• Schritt 4:

Allerdings sollten wir ein möglichst kurzes Programm schreiben. Glücklicherweise gelingt dies problemlos dank des Befehls repeat.

Wir betrachten nochmals unser langes Programm bei Schritt 3 und stellen fest, dass sich diese Befehlsfolgen 3 Mal wiederholen:

setpc red fd 100 rt 90 setpc yellow fd 100 rt 90 setpc red fd 100 rt 90 setpc yellow fd 100
pu bk 200 rt 90 pd

Wir fassen die beiden Teilprogrammen zusammen und wiederholen diese 3 Mal, um am Schluss die 3 farbigen Quadraten zu erhalten:

repeat 3 [setpc red fd 100 rt 90 setpc yellow fd 100 rt 90 setpc red fd 100 rt 90 setpc yellow fd 100 pu bk 200 rt 90 pd]

Nun haben wir unser Programm um einigen Befehlen verkürzt! Aber geht es noch kürzer?!

Überlege es dir und schicke uns deine Lösung per E-Mail an weekly-challenge (at) inf.ethz.ch.

Challenge 2

Diese Aufgabe verlangt, dass wir die Lösung zum gegebenen Bild mit repeat 4 […] beginnen sollen. Die erste Frage, die sich hierbei stellt, ist also, welches Muster sich im folgenden Bild vier mal versteckt:

Bei genauer Betrachtung sehen wir, dass das Bild sich in vier identische Muster zerlegen lässt bestehend aus je zwei Linien:

Bevor wir drauf los schiessen, überlegen wir uns zunächst unser Vorgehen anhand der folgenden drei Punkte:

1. Startposition
2. Grundmuster
3. Ausrichten

Alle drei Punkte wollen wir nun im Detail besprechen:

• Startposition: Wo beginnt der Weg und wie verläuft er?

Bevor wir die Aufgabe beginnen, müssen wir uns entscheiden, wo die Schildkröte ihren Weg beginnen soll. Es gibt viele Möglichkeiten und keine davon ist falsch. Im Bild unten sind vier verschiedene und zulässige Anfangspositionen der Schildkröte dargestellt. Wir haben uns hier für die Startposition (b) entschieden.

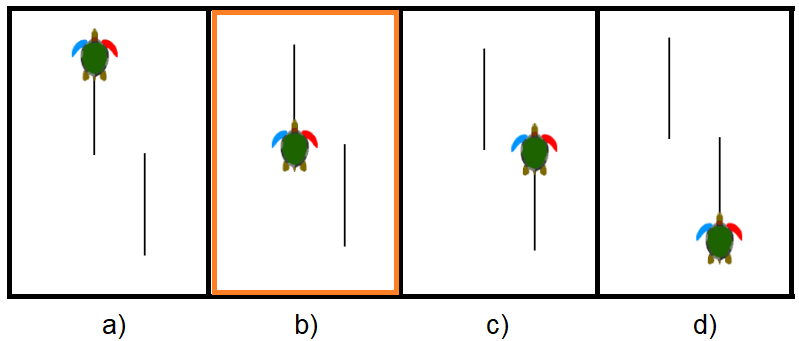
Soll das Muster von links nach rechts gezeichnet werden oder von rechts nach links? Abhängig davon, ob man die Startposition links oder rechts setzt, ergeben sich andere Lösungen. Wir haben uns hier dafür entschieden, das Muster links zu beginnen und nach rechts wachsen zu lassen (so wie dargestellt in der Abbildung links):

In unserem Fall beginnt die Schildkröte ihr Muster an der folgenden Stelle:

• Punkt 2: Wie zeichnet man das Grundmuster?

Nun da die Startposition feststeht und wir wissen, wie sich das Muster entwickeln soll, überlegen wir uns, wie man das oben abgebildete (orange umrandete) Grundmuster zeichnen kann ausgehend von der bereits gewählten Startposition. Wir finden das folgende Programm um die beiden Linien zu zeichnen:

fd 200 bk 200 
rt 90 
pu fd 100 pd
lt 90
bk 200 fd 200 

Danach steht die Schildkröte an der folgenden Stelle und hat erfolgreich sämtliche Linien im orange umrandeten Grundmuster gezeichnet, die restlichen Linien folgen bald… 😉

• Punkt 3: Wie richtet man die Schildkröte korrekt aus?

Nachdem das Grundmuster gezeichnet ist, stellt sich nun die Frage, wie man die Schildkröte danach wieder korrekt ausrichtet sodass sie wieder an der Startposition steht, jedoch beim zweiten Grundmuster. Gleich wie zuvor im ersten Muster, soll die Schildkröte auch im zweiten Muster wieder am unteren Ende der linken Linie starten. Die Schildkröte muss also von der aktuellen Position um 100 Schritte nach rechts gehen und darf dabei keine Spur hinterlassen:

Um diesen Weg hinter sich zu bringen, verwenden wir das folgende Programm:

rt 90 
pu fd 100 pd 
lt 90

Daraufhin steht die Schildkröte wieder in der identischen Lage wie am Anfnag, nur eben beim zweiten Muster. Wir sind nun bereit die bisherigen Teile zu wiederholen...

Zusammenfassung:

Wenn man nun alle bisherigen Punkte zusammenfasst, so lässt sich das Muster mit den zusammengesetzten Lösungen aus Punkt 2 und 3 wie folgt beschreiben:

fd 200 bk 200 rt 90 pu fd 100 pd lt 90 bk 200 fd 200 rt 90 pu fd 100 pd lt 90
fd 200 bk 200 rt 90 pu fd 100 pd lt 90 bk 200 fd 200 rt 90 pu fd 100 pd lt 90
fd 200 bk 200 rt 90 pu fd 100 pd lt 90 bk 200 fd 200 rt 90 pu fd 100 pd lt 90
fd 200 bk 200 rt 90 pu fd 100 pd lt 90 bk 200 fd 200 rt 90 pu fd 100 pd lt 90

Oder kurz:

repeat 4 [fd 200 bk 200 rt 90 pu fd 100 pd lt 90 bk 200 fd 200 rt 90 pu fd 100 pd lt 90]

Challenge 3

Diese Aufgabe sieht schwieriger aus, als sie ist. Vor allem, weil es so aussieht, als ob es nicht genug Informationen gibt. Aber die Zeichnung gibt mehr, als es scheint. Wir haben ein 700 x 700 Quadrat und ein 100 x 100 Quadrat in der Mitte. Dieses Quadrat kann sich in der Mitte des grossen Quadrats befinden, wenn und nur wenn alle Rechtecke, aus denen dieses Bild besteht, gleich gross sind.

Schritt 1: Lasst uns sehen, welche Informationen wir aus diesem Bild herausholen können.

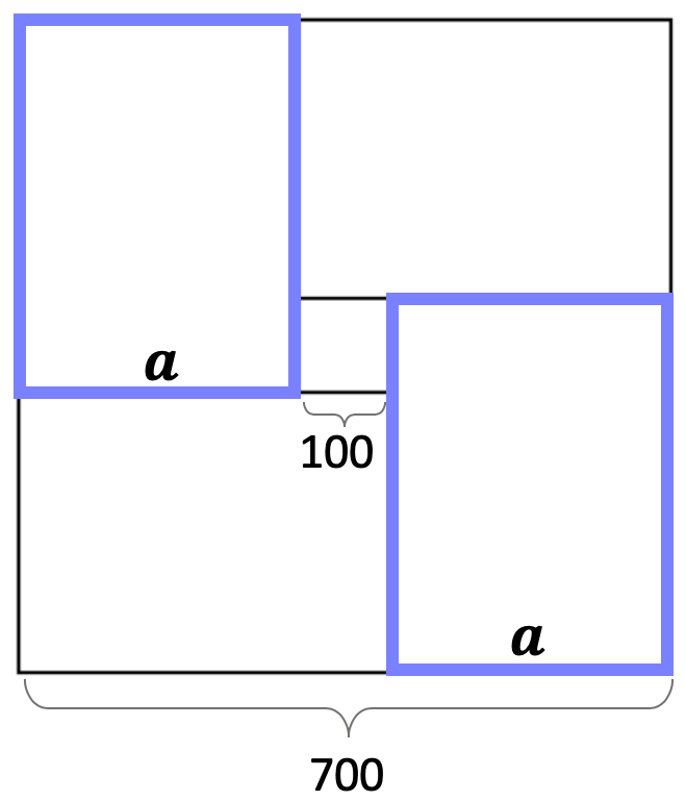
Schauen wir uns die markierten Rechtecke an. Aus der Zeichnung kann man erkennen, dass die Addition der kürzeren Seiten «a» des Rechtecks oben links und unten rechts und der Seite des kleinen Quadrats die Seite des grösseren Quadrats ergibt:

a + a + 100 = 700

2a = 700 - 100

2 a = 600

a = 300

Dies bedeutet, dass die Seite «a» des Rechtecks 300 betragen muss.

Schritt 2:

Die Bestimmung der Länge der längeren Seite b von Rechtecken steht noch aus. Schauen wir uns nun die Zeichnung an:

Aus der Zeichnung kann man erkennen, dass die Summe der kürzeren Seite des unteren linken Rechtecks und der längeren Seite des oberen linken Rechtecks 700 ergibt.

a + b = 700

Aus dem Schritt 1 wissen wir, dass Seite a = 300. Daher erhalten wir die längere Seite des Rechtecks:

b = 700 - a

b = 400

Bisher haben wir festgestellt, dass alle vier Rechtecke identisch sein müssen und dass die kürzere Seite der Rechtecke a = 300 und die längere Seite b = 400. Also haben wir alle Informationen benötigt, die wir zum Zeichnen des Bildes brauchten.

Schritt 3: Wie genau das Programm aussehen wird, hängt vom Ausgangspunkt ab. Beginnen wir zum Beispiel an dem Punkt, an dem die Schildkröte im Bild positioniert ist.

Das grosse Quadrat ist aus vier Rechtecken zusammengesetzt. Um das Bild zu zeichnen, muss die Schildkröte ein Rechteck nach dem anderen zeichnen. Und nachdem das erste Rechteck gezeichnet ist, wird das nächste Rechteck um 90 Grad gegenüber dem vorhergehenden Rechteck gedreht.

Nun wollen wir das erste Rechteck zeichnen - das obere linke. Die Schildkröte beginnt wie in der Zeichnung dargestellt. Das Programm zum Zeichen des ersten Rechtecks ist:

repeat 2 [fd 400 rt 90 fd 300 rt 90] 

Das Rechteck wird gezeichnet und die Schildkröte befindet sich nun wieder in der Startposition. Eine einfache Drehung des Rechtecks um 90 Grad wäre nicht korrekt. Wir müssen die Schildkröte so positionieren, wie in der Zeichnung dargestellt:

Diese Positionierung der Schildkröte zum Zeichnen des nächsten Rechtecks erfolgt durch:

fd 400 rt 90 fd 300

Von da an müssen wir das gleiche Rechteck noch einmal wiederholen:

repeat 2 [fd 400 rt 90 fd 300 rt 90] 

Dieser Schritt brachte uns in die Startposition wieder.

Von dort aus müssen wir die Schildkröte neu positionieren und das nächste Rechteck zeichnen.

fd 400 rt 90 fd 300

repeat 2 [fd 400 rt 90 fd 300 rt 90] 

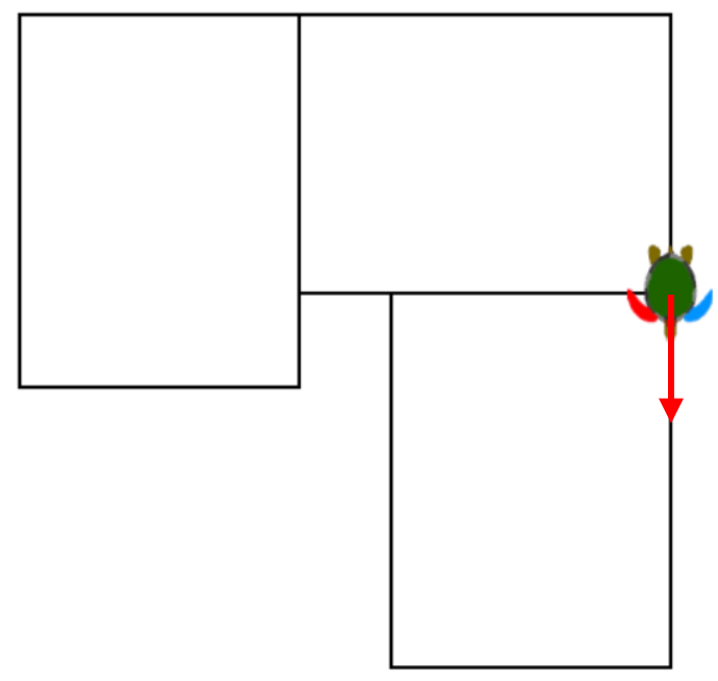
Und schliesslich die Neupositionierung und das Zeichnen des Rechtecks mit:

fd 400 rt 90 fd 300
repeat 2 [fd 400 rt 90 fd 300 rt 90] 

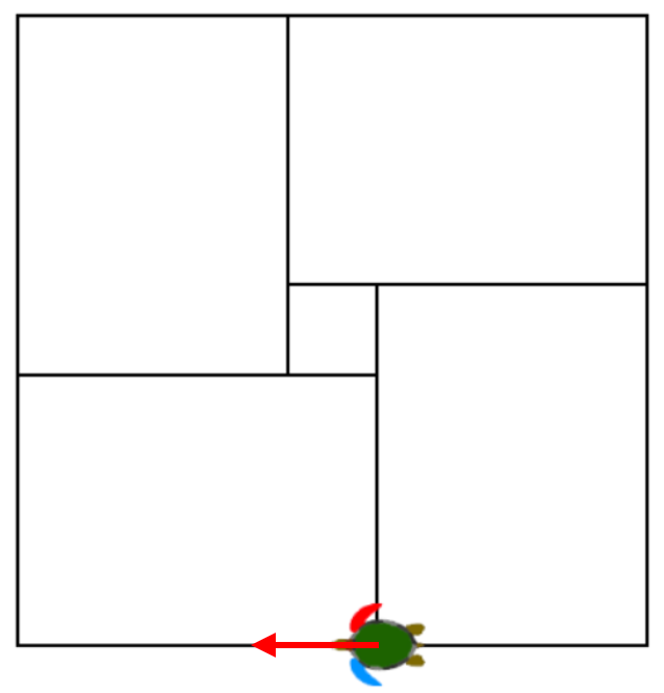
Und endlich mit:

fd 400 rt 90 fd 300

haben wir die Schildkröte in die Startposition gebracht.

Zusammenfassung:

So sieht unser Programm aus:

repeat 2 [fd 400 rt 90 fd 300 rt 90] 
fd 400 rt 90 fd 300

repeat 2 [fd 400 rt 90 fd 300 rt 90] 
fd 400 rt 90 fd 300

repeat 2 [fd 400 rt 90 fd 300 rt 90] 
fd 400 rt 90 fd 300

repeat 2 [fd 400 rt 90 fd 300 rt 90] 
fd 400 rt 90 fd 300

Oder kürzer geschrieben mit Hilfe des Befehls Repeat innerhalb des Befehls repeat:

repeat 4[ repeat 2 [fd 400 rt 90 fd 300 rt 90] fd 400 rt 90 fd 300]

Beiträge von euch

Hier präsentieren wir ein paar ausgewählte Beiträge, die uns per E-Mail erreicht haben:

Vielen Dank für eure Teilnahme und das Einsenden eurer tollen Lösungen!

Kalenderwoche 17/18

Diese Challenge läuft von Mittwoch, dem 22. April 2020, bis Dienstag, dem 28. April 2020. Am Mittwoch, dem 29. April 2020, laden wir einen Lösungsvorschlag hoch.

Tutorial

Diese Woche werden wir der Schildkröte neue Wörter beibringen (anstatt sie uns, wie in den vergangenen Wochen). Dazu verwenden wir den Editor links, wo beliebig viele neue Befehle definiert werden können. Um einen dieser Befehle anschliessend zu verwenden, schreiben wir seinen Namen in die Befehlszeile oben rechts.

Wir verwenden weiterhin die Programmierumgebung XLogoOnline (opens new window) und bearbeiten nun im Übungsheft (opens new window) die Aufgaben 17-25 (Kapitel 3, Programme benennen und aufrufen).

Übersicht

Wir lernen, den Wortschatz der Schildkröte mit unseren eigenen Befehlen zu erweitern. Dies erlaubt uns, häufig verwendete Programme (zum Beispiel Quadrate oder Rechtecke) unter einem Namen abzuspeichern, um sie später schnell und einfach aufrufen zu können.

Bisher mussten wir die folgenden Befehle schreiben, um ein Quadrat der Seitenlänge 100 zu zeichnen: repeat 4 [fd 100 rt 90]

Neu können wir diesem Programm einen Namen zuweisen (zum Beispiel quadrat). Dies tun wir im Editor links:

Um dein Programm aufzurufen, schreibst du einfach dessen Namen in die Eingabezeile rechts:

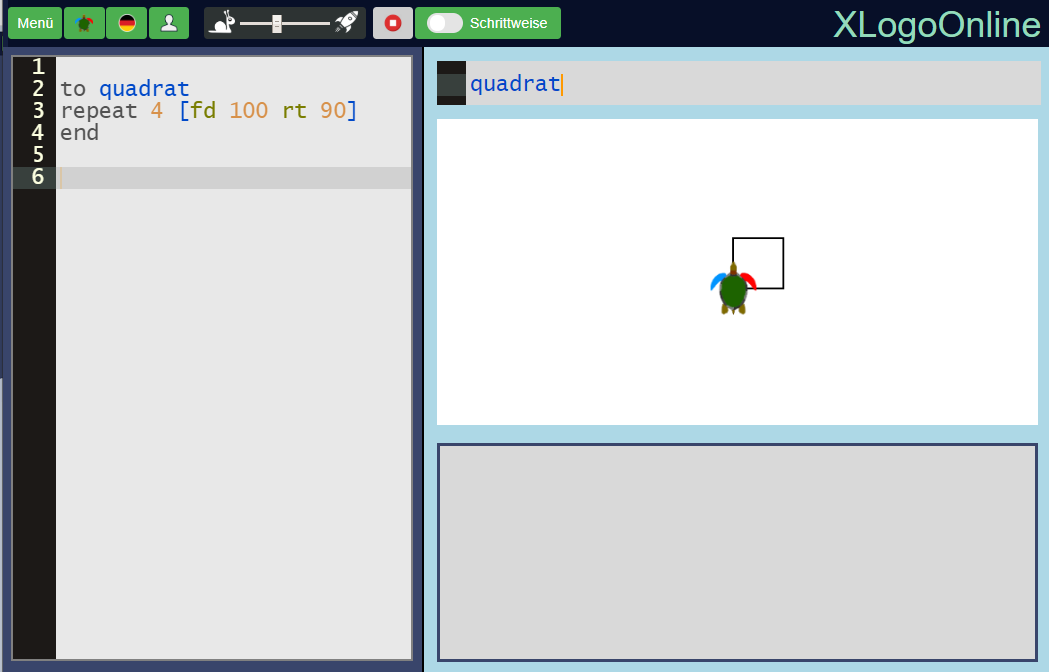
Auf diese Weise kannst du nun neben bereits bekannten Befehlen wie fd und bk auch deine eigenen Befehle verwenden und umso grössere und komplexere Bilder zeichnen.

Challenge

Diese Woche werden wir auch nicht versäumen, euch neue Probleme zu präsentieren:

Tobe dich aus

Schreibe mit der Schildkröte deinen Namen. Definiere für jeden darin verwendeten Buchstaben einen eigenen Befehl mit dem Namen buchstabe_a, buchstabe_b, buchstabe_c, ..., buchstabe_z. Schick uns dein Bild per E-Mail an weekly-challenge (at) inf.ethz.ch.

Lösung anzeigen

Challenge 1

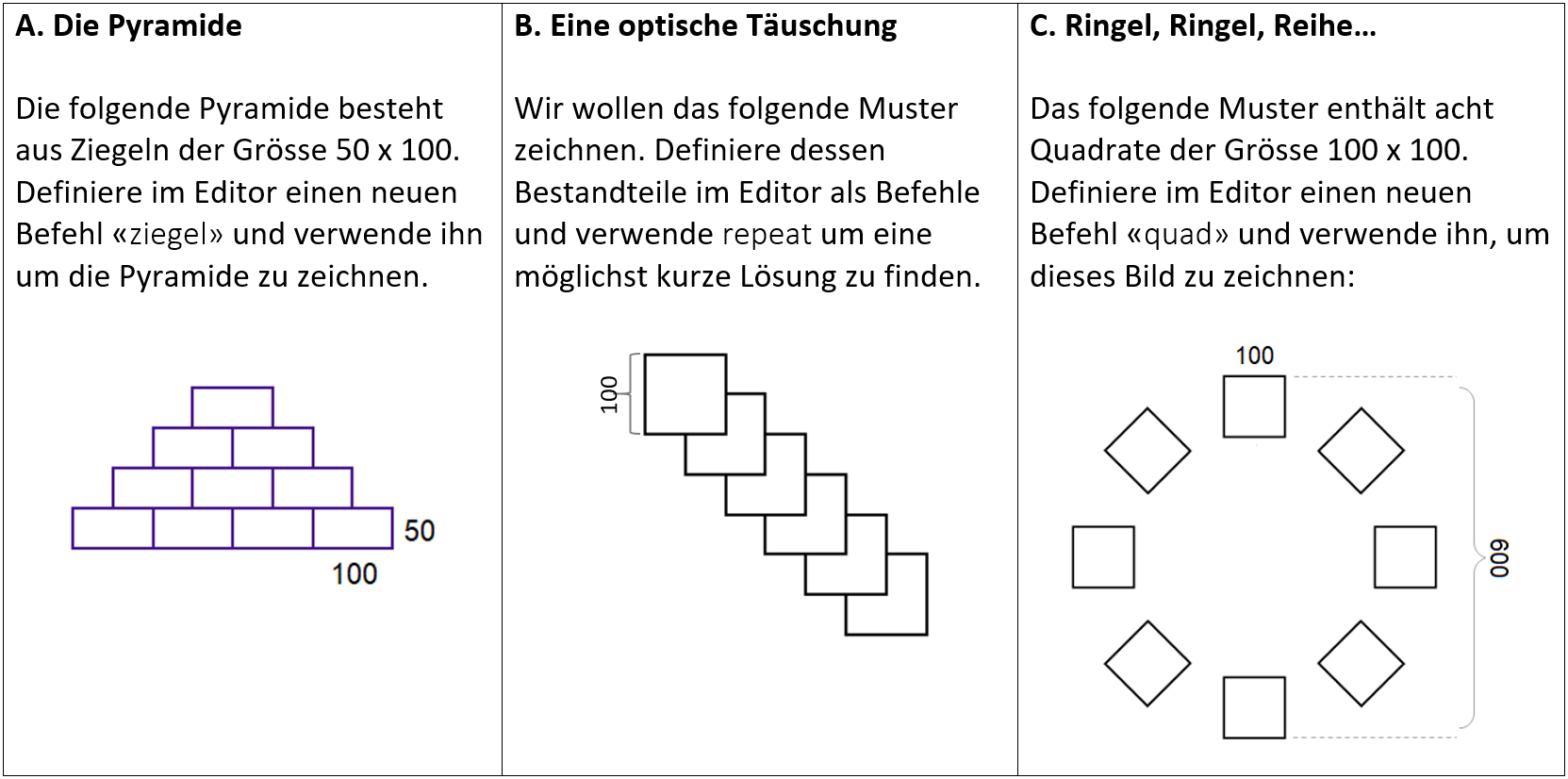
Schauen wir, wie diese Aufgabe am einfachsten zu lösen ist. Wir haben nur ein Element, das wir programmieren und wiederholen müssen, um die Pyramide zu bauen - den Ziegel.

Zuerst schreiben wir das Programm ziegel im Editor. Mit diesem haben wir einen neuen Befehl definiert, der das Element unserer Pyramide zeichnet.

to ziegel
setpc 15
repeat 2 [fd 50 rt 90 fd 100 rt 90] 
end

Nach der Eingabe des neu definierten Befehls ziegel im Eingabefeld zeichnet die Schildkröte einen violetten Ziegelstein und kommt in die Ausgangsposition zurück.

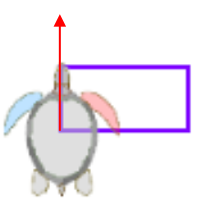
Um den nächsten Ziegelstein zu zeichnen, muss man die Schildkröte in die richtige Position bringen und den Befehl ziegel erneut eingeben. Damit die Schildkröte in die richtige Position gebracht wird, gibt man folgende Befehle in das Eingabefeld ein:

rt 90 fd 100 lt 90

Wir wiederholen den Befehl ziegel und die Neupositionierung, bis wir die erste Reihe von Steinen gezeichnet haben.

ziegel rt 90 fd 100 lt 90

ziegel rt 90 fd 100 lt 90

und noch einmal:

ziegel rt 90 fd 100 lt 90

Das Programm für das Zeichnen der ersten vier Steine sieht so aus:

ziegel rt 90 fd 100 lt 90
ziegel rt 90 fd 100 lt 90
ziegel rt 90 fd 100 lt 90
ziegel rt 90 fd 100 lt 90

Oder wir können auch den Befehl repeat verwenden und dieses Programm kürzer schreiben:

repeat 4 [ziegel rt 90 fd 100 lt 90]

Um den nächsten von drei Ziegeln zu zeichnen, muss die Schildkröte nun auf die erste Ziegelreihe klettern und in der Mitte der Oberseite des ersten Ziegels beginnen, wie auf dem Bild:

Um dies zu tun, müssen wir Folgendes eingeben:

fd 50 lt 90 fd 350 rt 90

Jetzt ziehen wir die zweite Ziegelreihe, aber diesmal nur mit drei Ziegeln:

ziegel rt 90 fd 100 lt 90
ziegel rt 90 fd 100 lt 90
ziegel rt 90 fd 100 lt 90

Oder kürzer:

repeat 3 [ziegel rt 90 fd 100 lt 90]

Um die Schildkröte für die neue Ziegelreihe auszurichten, schreiben wir:

fd 50 lt 90 fd 250 rt 90

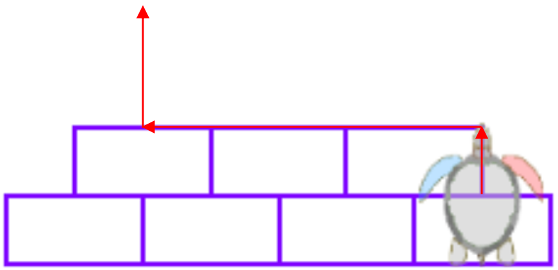
Es folgt die dritte Ziegelreihe:

ziegel rt 90 fd 100 lt 90
ziegel rt 90 fd 100 lt 90

Oder:

repeat 2 [ziegel rt 90 fd 100 lt 90]

Ausrichten:

fd 50 lt 90 fd 150 rt 90

Und schliesslich der allerletzte Ziegelstein:

ziegel

Zusammenfassung:

Um die dargestellte Pyramide zu bauen, haben wir zunächst einen neuen Befehl zum Zeichnen eines Ziegels im Editor definiert. Diesen Ziegelstein haben wir 10 Mal verwendet. Um Ziegelsteine an den richtigen Stellen zu zeichnen, müssen wir die Schildkröte vorsichtig neu positionieren und dann einfach den Befehl ziegel aufrufen. Damit kommen wir zum folgenden Programm:

to ziegel
setpc 15
repeat 2 [fd 50 rt 90 fd 100 rt 90] 
end

Erste Reihe:

repeat 4 [ziegel rt 90 fd 100 lt 90]

Zweite Reihe:

fd 50 lt 90 fd 350 rt 90
repeat 3 [ ziegel rt 90 fd 100 lt 90]

Dritte Reihe:

fd 50 lt 90 fd 250 rt 90
repeat 2 [ ziegel rt 90 fd 100 lt 90]

und der letzte Ziegel:

fd 50 lt 90 fd 150 rt 90
ziegel

Challenge 2

Das Bild zeigt 6 Quadrate: Fünf zum Teil mit dem darüber liegenden Quadrat bedeckt und ein vollständig sichtbares Quadrat ganz oben. Da wir fünf identische Elemente haben, ist es sicher sinnvoll, einen neuen Befehl zu definieren, der nur dieses Element zeichnet. Wir können dies im Editor tun. Das teilweise bedeckte quadratische Element kann man auf verschiedene Arten programmieren. Hier werden wir es zeichnen, indem wir die Befehle pu und pd zusätzlich zu den Befehlen fd, rt, lt und repeat verwenden. Wir sehen dieses Element als ein Quadrat mit teilweise unsichtbaren Seiten.

Das Programm zum Zeichnen des Elements sieht wie folgt aus:

to quadbiss
fd 50 pu fd 50 rt 90 fd 50 pd fd 50 rt 90 fd 100 rt 90 fd 100 rt 90
end

Der Start- und Endpunkt des Weges der Schildkröte ist die linke untere Ecke, so wie wir ein reguläres Quadrat zeichnen. Der nächste Schritt ist die richtige Positionierung der Schildkröte für das Zeichnen des nächsten Elements:

Wir können die Schildkröte mit den folgenden Befehlen in die korrekte Position bringen:

pu fd 50 lt 90 fd 50 rt 90 pd

Von hier aus müssen wir die neu definierte Funktion quadbiss und den Befehlssatz für die Neupositionierung der Schildkröte aufrufen, und wir erhalten ein zweites Quadrat über dem ersten.

quadbiss
pu fd 50 lt 90 fd 50 rt 90 pd

Um alle 5 teilweise bedeckten Quadrate zu zeichnen, wiederholen wir den gleichen Befehlssatz noch drei Mal:

quadbiss
pu fd 50 lt 90 fd 50 rt 90 pd

quadbiss
pu fd 50 lt 90 fd 50 rt 90 pd

quadbiss
pu fd 50 lt 90 fd 50 rt 90 pd

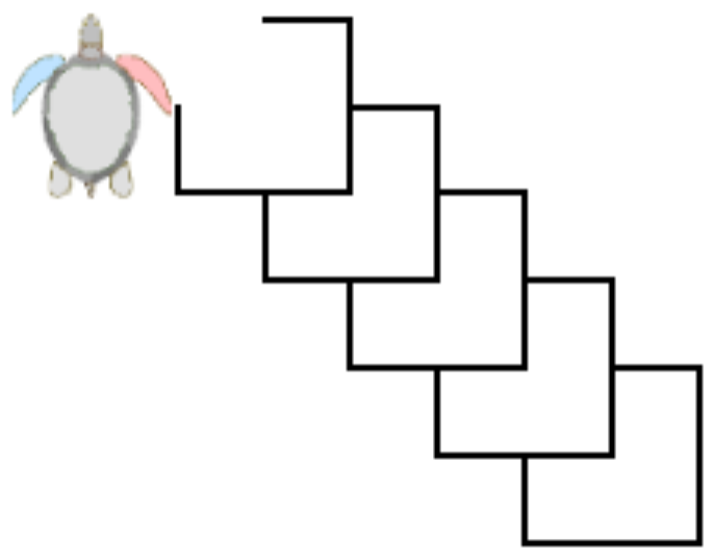
Alles, was noch zu tun übrig bleibt, ist, ein letztes Quadrat darauf zu zeichnen.

repeat 4 [fd 100 rt 90]

Zusammenfassung:

Um dieses Bild zu zeichnen, haben wir Folgendes getan:

1. Wir haben einen neuen Befehl quadbiss definiert, der ein "teilweise bedecktes" quadratisches Element zeichnet.
2. Wir haben die Schildkröte neu positioniert, so dass wir nur den Befehl quadbiss aufrufen müssen, um das nächste Element zu zeichnen.
3. Wir haben Schritt 1 und Schritt 2 fünf Mal wiederholt.
4. Ganz zuletzt zeichnen wir ein normales Quadrat.

In Xlogo sieht dies so aus:

Im Editor:

to quadbiss
fd 50 pu fd 50 rt 90 fd 50 pd fd 50 rt 90 fd 100 rt 90 fd 100 rt 90
end

Im Eingabefeld:

quadbiss
pu fd 50 lt 90 fd 50 rt 90 pd

quadbiss
pu fd 50 lt 90 fd 50 rt 90 pd

quadbiss
pu fd 50 lt 90 fd 50 rt 90 pd

quadbiss
pu fd 50 lt 90 fd 50 rt 90 pd

quadbiss
pu fd 50 lt 90 fd 50 rt 90 pd

repeat 4 [fd 100 rt 90]

Dies können wir kürzer schreiben, indem wir den Befehl repeat verwenden:

repeat 5 [quadbiss pu fd 50 lt 90 fd 50 rt 90 pd]
repeat 4 [fd 100 rt 90]

Challenge 3

Diese Aufgabe fordert uns auf, acht Quadrate der Grösse 100 x 100 im Kreis anzuordnen und zudem sicherzustellen, dass der Kreis am Schluss einen Durchmesser von 600 Schritten hat. Der schwierigste Aspekt dieser Aufgabe ist nicht die Frage, wie wir einen neuen Befehl quad anlegen, mit welchem wir Quadrate der Grösse 100 x 100 zeichnen können, sondern vielmehr, wie man anschliessend die acht Quadrate im Kreis anordnet. Wir erklären das Vorgehen in einzelnen Schritten:

1. Beginnen wir mit dem einfachsten Schritt: Wir wollen einen neuen Befehl mit dem Namen quad definieren, welcher ein Quadrat der Seitenlänge 100 zeichnet. Das Programm um ein solches Quadrat zu zeichnen lautet repeat 4 [fd 100 rt 90] und wir weisen ihm anschliessend im Editor links den Namen quad zu:

to quad
repeat 4 [fd 100 rt 90]
end

Diesen Befehl können wir nun nach Belieben verwenden um Quadrate zu zeichnen, indem wir rechts in der Eingabezeile den Befehl quad verwenden.

2. Nun stellt sich die Frage, wie man mit dem neuen Befehl das gegebene Muster zeichnen kann. Mehrere Ansätze mit verschiedenen Startpositionen sind denkbar, aber nicht alle davon sind gleich einfach umzusetzen... Einer der schwieriger umzusetzenden Ansätze ist derjenige, welcher versucht den Umfang des Kreises abzufahren und an den passenden Stellen ein Quadrat zu zeichnen:

Es ist äusserst schwierig, die Distanz zwischen zwei Quadraten abzuschätzen und am Schluss dennoch einen Kreis mit Radius 600 zu zeichnen. Wir müssten im folgenden Programm angeben können, wie weit die Schildkröte vorwärts zu gehen hat, was wir mit fd ??? kennzeichnen:

repeat 8 [quad rt 90 fd 100 rt 45 pu fd ??? lt 90 pd]

Ein wesentlich einfacherer Ansatz wäre es, dass wir der Startpunkt nicht auf dem Kreis selbst wählen, sondern im Mittelpunkt des Kreises:

Wir wissen, dass die Distanz vom Mittelpunkt bis zum oberen Ende der Quadrate 300 Schritte beträgt. Das Quadrat selbst ist 100 Schritte hoch. Somit muss die Schildkröte also vom Mittelpunkt aus zunächst 200 Schritte im Wandermodus nach aussen gehen, um auf der unteren Kante eines Quadrates zu stehen:

pu
fd 200
pd

Jetzt befindet sich die Schildkröte genau in der Mitte der unteren Kante. Wir wissen, dass der Befehl quad dazu führt, dass ein Quadrat der Seitenlänge 100 gezeichnet wird, wobei die aktuelle Position der linken unteren Ecke entspricht. Um diesen Befehl verwenden zu können, müssen wir also zunächst an diejenige Position laufen, wo sich die linke untere Ecke befinden wird. Konkret heisst das: Wir müssen 50 Schritte nach links...

pu
fd 200
pd

lt 90
fd 50
rt 90

An dieser Stelle können wir nun den neuen Befehl quad verwenden und zeichnen damit das Quadrat:

pu
fd 200
pd

lt 90
fd 50
rt 90

quad

Anschliessend fahren wir auf demselben Weg wieder zurück zum Mittelpunkt, von wo aus wir gestartet sind:

pu
fd 200
pd

lt 90
fd 50
rt 90

quad

rt 90 
fd 50
lt 90

pu
bk 200
pd

Um das nächste Quadrat zu erreichen, müssen wir die Schildkröte rotieren. Sie dreht sich insgesamt einmal um die eigene Achse (am Anfang schaut sie nach oben, ebenso wie am Ende, wenn sie das vollständige Muster gezeichnet hat – unterwegs macht sie eine Pirouette um ihre eigene Achse). Die 360° dieser Umdrehung werden in acht identische Segmente unterteilt:

Wenn wir die 360° auf 8 Segment aufteilen, erhalten wir pro Segment eine Drehung von 360°/8 = 45°, die die Schildkröte jeweils nach jedem Segment drehen muss. Wir erweitern unsere bisherige Lösung also mit einer Rechtsdrehung um 45 Grad (eine Linksdrehung wäre ebenfalls möglich):

pu
fd 200
pd

lt 90
fd 50
rt 90

quad

rt 90 
fd 50
lt 90

pu
bk 200
pd

rt 45

Dasselbe Programm können wir nun acht Mal wiederholen, um das vollständige Muster zu zeichnen. Wir schreiben dies wie folgt:

repeat 8 [pu fd 200 pd lt 90 fd 50 rt 90 quad rt 90 fd 50 lt 90 pu bk 200 pd rt 45]

Und erhalten schliesslich das vollständige Muster.

Beiträge von euch

Hier präsentieren wir ein paar ausgewählte Beiträge, die uns per E-Mail erreicht haben:

Vielen Dank für eure Teilnahme und das Einsenden eurer tollen Lösungen!

Kalenderwoche 18/19

Diese Challenge läuft von Mittwoch, dem 29. April 2020, bis Dienstag, dem 5. Mai 2020. Am Mittwoch, dem 6. April 2020, laden wir einen Lösungsvorschlag hoch.

Tutorial

Wir verwenden weiterhin die Programmierumgebung XLogoOnline (opens new window) und bearbeiten nun im Übungsheft (opens new window) die Aufgaben 26-37 (Kapitel 3, Programme benennen und aufrufen).

Übersicht

Bisher hast du gelernt, mithilfe von Befehlen wie fd und rt Programme zu bauen. Ein Programm ist im Prinzip nichts anderes als eine Abfolge von Befehlen.

Letzte Woche haben wir gelernt, dass man solchen Folgen von Befehlen auch einen Namen geben kann. Wir schreiben dazu im Editor:

to name
befehle...
end 

Ab diesem Moment kennt die Schildkröte einen neuen Befehl name - dieser erlaubt uns, das darin abgelegte Programm schnell und einfach wieder aufzurufen. Auf diese Weise können beliebig viele neue Befehle definiert werden, die ihrerseits wieder zu längeren Programmen zusammengesetzt und benannt werden können. Dasselbe Prinzip kennen wir auch ausserhalb des Computers: Ein Fahrrad besteht aus vielen Einzelteilen, die zuerst zusammengestellt werden müssen, bevor das Fahrrad fährt.

Es ist nützlich, neue Befehle anzulegen um wiederholende Muster zu zeichnen, grosse und komplexe Figuren zu zeichnen und um die Lesbarkeit eines Programms zu erhöhen. Ein Befehl, welcher in einem anderen Befehl verwendet wird, bezeichnen wir als dessen Unterprogramm. Das folgende Diagramm stellt dar, wie das Programm tausendfüssler aus den Unterprogrammen rumpf und kopf aufgebaut ist, die ihrerseits wieder Unterprogramme enthalten:

Challenge

Auch diese Woche erwarten dich wieder drei knifflige Challenges:

Tobe dich aus

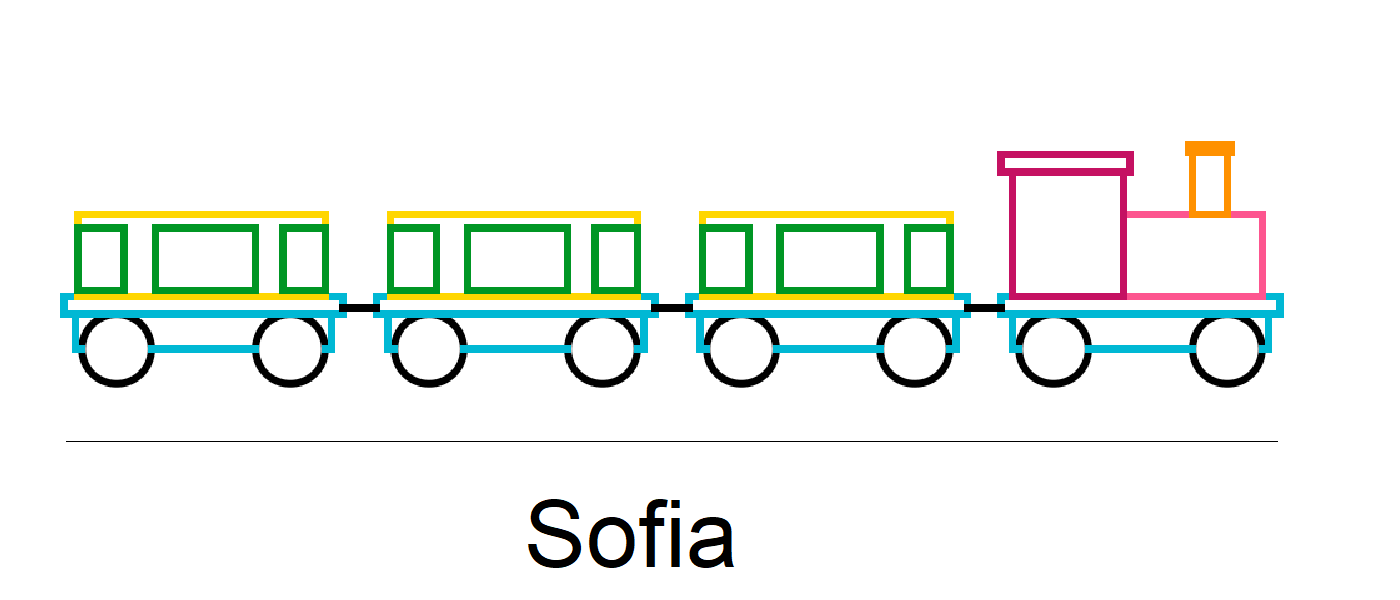
Wir zeichnen einen alten Dampfzug! Gestalte eine Lokomotive und einen Wagen. Speichere die beiden unter den Namen lokomotive und wagen. Zeichne dann einen Dampfzug mit einer Lokomotive, gefolgt von drei Wagen. Speichere den vollständigen Zug am Schluss unter dem Namen dampfzug.

Schick uns dein Bild und das Programm per E-Mail an weekly-challenge (at) inf.ethz.ch.

Lösung anzeigen

Challenge A: Traumhaus

Bei dieser Aufgabe geht es darum, drei Unterprogramme zu definieren und diese in ein Hauptprogramm zu integrieren, sodass am Schluss nur der Befehl haus eingegeben werden muss, um das gelb-rote Haus als Abbildung zu erhalten. Wir lösen das Problem in vier Schritten:

Schritt 1

Wir definieren den unteren Teil des Hauses – ein gelbes Quadrat. Die Seitenlängen kennen wir, sie betragen 100 Schritte. Mit dem Befehl repeat schreiben wir eine möglichst kompakte Lösung. Zum Start setzen wir die Schildkröte auf die linke untere Ecke des Quadrats, wo sie nach oben schaut.

to quadrat
repeat 4 [setpc yellow fd 100 rt 90]
end

Nachdem wir das Programm ausgeführt haben, erhalten wir das folgende Bild:

Schritt 2

Nun definieren wir das Dach des Hauses – ein rotes Dreieck. Auch hier kennen wir die Seitenlänge, sie beträgt jeweils 100 Schritte. Die Herausforderung ist hier die Ausrichtung der Schildkröte, bevor sie mit dem Zeichnen des roten Dreiecks beginnt.

Wir entscheiden uns dafür, die Schildkröte unten rechts wie in der folgenden Abbildung zu positionieren:

Das Programm schreiben wir wieder mithilfe des Befehls repeat. Weil ein Dreieck drei Seiten besitzt, schreiben wir repeat 3. Weiter besitzt ein Dreieck auch drei Ecken. Aus diesem Grund schreiben wir rt 360/3 für die Drehung. Alternativ kann man statt rt 360/3 auch rt 120 verwenden.

to dreieck
lt 90 repeat 3 [fd 100 rt 360/3]
end

Nachdem das Programm ausgeführt wurde, befindet sich die Schildkröte an de folgenden Position:

Schritt 3

Nun brauchen wir ein Programm für die Ausrichtung unserer Schildkröte. Hans' Programm verwendet diesen Befehl, um zwischen dem Quadrat und dem Dreieck die Position zu wechseln. Die drei Unterprogramme quadrat, ausrichten und dreieck sollen am Schluss zu einem Haus vereint werden können...

Wir erinnern uns, am Ende der Ausführung von quadrat befindet sich die Schildkröte an der folgenden Stelle:

Weil sich die Schildkröte nach der Ausführung des Unterprogramms dreieck an der folgenden Stelle befindet...

... muss sie nach dem Zeichnen von quadrat also geschickt die Position wechseln und zur Ausgangsposition des Dreiecks laufen:

Dafür schreiben wir das folgende Unterprogramm:

to ausrichten
pu fd 100 rt 90 fd 100 lt 90 pd
end

Schritt 4

Nun führen wir alle 3 Unterprogramme zusammen, so wie es Hans in seinem Hauptprogramm haus vorgegeben hat:

to haus
quadrat
ausrichten
dreieck
end

... und erhalten am Schluss das folgende Bild:

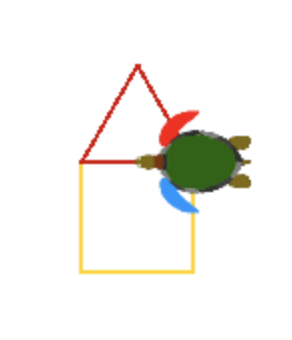
Hans dankt dir von Herzen für deine tolle Unterstützung! 😃

Challenge B: Tanzende Quadrate

Bisher hast gelernt, wie du den Wortschatz deiner Schildkröte erweitern kannst, indem du deine eigenen Befehle definierst und benennst. Diese Befehle können auch kurze Programme sein, die innerhalb eines grösseren Programms verwendet werden können. Dafür brauchst du nur ihre Namen aufzurufen und schon werden diese Befehle ausgeführt. In dieser Aufgabe solltest du das Bild mit drei Befehlen zeichnen: quadblau, quadrot und muster. Der Befehl muster ist das Hauptprogramm, in dem wir die Unterprogramme quadblau und quadrot und einige andere reguläre Befehle, die du verwendest, wie fd, lt, rt, pu oder pd, aufrufen werden.

to quadrot
setpc red
repeat 4 [fd 200 rt 90]
end

Um das rote Quadrat wie auf dem Bild zu zeichnen, muss man die Schildkröte vor dem Start des Programms um 45 Grad nach rechts drehen. Nachdem man rt 45 quadrot in das Eingabefeld eingetragen hat, zeichnet unsere Schildkröte das folgende Bild:

Wir wollen nun das erste blaue Quadrat zeichnen. Dieses berührt mit seiner unteren rechten Ecke die Mitte der Seite des roten Quadrats. Um an diesen Punkt zu kommen, sollte die Schildkröte im Wandermodus 100 Schritte vorwärts gehen (siehe Bild (a)). Danach sollte sie sich um 45 Grad nach links drehen (siehe Bild (b)).

 pu fd 100 lt 45

Wenn wir das Programm so einfach wie möglich gestalten wollen, dann ist es besser, das blaue Quadrat durch eine Links- anstatt durch eine Rechtsdrehung zu zeichnen.

to quadblau
setpc blue
repeat 4 [fd 100 lt 90]
end

Nach Aufruf des Befehls quadblau erhalten wir die Situation, welche unten in Bild (c) dargestellt ist:

Nun müssen wir die Schildkröte um 45 Grad nach rechts zurückdrehen und wieder 100 Schritte im Wandermodus laufen. Wenn sich die Schildkröte danach um 90 Grad nach rechts dreht, kommt sie in eine Position, die für die weiteren Schritte praktisch ist (dargestellt oben in Bild (d)).

Von diesem Zeitpunkt an brauchen wir nur noch die Befehle zu wiederholen, die wir zuvor geschrieben haben, um ein zweites blaues Quadrat zu erstellen:

fd 100 lt 45 pd  quadblau rt 45 pu fd 100 rt 90

Um ein drittes blaues Quadrat zu zeichnen:

fd 100 lt 45 pd  quadblau rt 45 pu fd 100 rt 90

Und um ein viertes blaues Quadrat zu zeichnen:

fd 100 lt 45 pd  quadblau rt 45 pu fd 100 rt 90

Um die vier blauen Quadrate und das grosse rote Quadrat zu zeichnen, haben wir Folgendes ausgeführt:

rt 45 quadrot
fd 100 lt 45 pd quadblau rt 45 pu fd 100 rt 90
fd 100 lt 45 pd quadblau rt 45 pu fd 100 rt 90
fd 100 lt 45 pd quadblau rt 45 pu fd 100 rt 90
fd 100 lt 45 pd quadblau rt 45 pu fd 100 rt 90

Oder kürzer geschrieben:

rt 45 quadrot
repeat 4 [ fd 100 lt 45 pd quadblau rt 45 pu fd 100 rt 90 ]

Und der letzte Schritt ist die Definition des allerletzten Befehls (nämlich unseres Hauptprogramms muster):

to muster
rt 45 quadrot
repeat 4 [ fd 100 lt 45 pd quadblau rt 45 pu fd 100 rt 90 ]
end

Zusammenfassung

Um die Aufgabe zu erfüllen, haben wir zwei neue Befehle definiert - mit anderen Worten, wir haben zwei kurze Programme geschrieben, um das rote Quadrat und die vier blauen Quadrate zu zeichnen:

to quadrot
setpc red
repeat 4 [fd 200 rt 90]
end

to quadblau
setpc blue
repeat 4 [fd 100 lt 90]
end

Und schliesslich ist der dritte Befehl das eigentliche Programm, das die beiden Unterprogramme quadrot und quadblau umfasst:

to muster
rt 45 quadrot
repeat 4 [ fd 100 lt 45 pd quadblau rt 45 pu fd 100 rt 90 ]
end

Challenge C: Blumenwiese

Das Bild der Blumenwiese scheint auf den ersten Blick sehr komplex – es besteht aus sehr vielen einzelnen Komponenten und die Gefahr sich zu verlieren ist gross. Aus diesem Grund zerlegen wir das Bild hier (wie in der Aufgabenstellung vorgeschlagen) in einzelne Komponenten, welche wir einzeln testen und dann zusammensetzen. Generell beginnen wir bei solchen Aufgaben immer mit den kleinsten Komponenten (es ist beispielsweise viel einfacher, sich zuerst mal nur um ein Blatt zu kümmern, bevor man gleich die ganze Blüte mit vielen Blättern zeichnet). Wir befolgen hier also die Reihenfolge, welche in der Aufgabenstellung vorgeschlagen wird, und arbeiten uns von kleinen Elementen langsamen zu den grösseren Elementen. Wir zerlegen die Blumenwiese in die folgenden Teile, welche wir in dieser Reihenfolge erarbeiten werden: quadrat, stiel, blüte, blume, wiese:

1. Wir schreiben das Programm quadrat:

Der Start ist denkbar einfach. Das Programm für ein Quadrat haben wir inzwischen schon einige Male gesehen: repeat 4 [fd 100 rt 90]. Wir wissen auch, wie wir diesem Programm einen Namen geben können:

to quadrat
repeat 4 [fd 100 rt 90]
end

Ab diesem Moment steht uns der Befehl quadrat neu zur Verfügung und wir können ihn nach eigenem Bedarf dazu verwenden, um Bilder zu zeichnen, welche das Muster eines Quadrates enthalten.

2. Wir schreiben das Programm stiel:

Auch das Programm stiel ist vergleichbar einfach, denn der Stiel ist nichts anderes als eine grüne Linie der Länge 400. Das Programm dazu lautet also: setpc green fd 400. Auch diesem Programm wollen wir nun einen Namen geben, nämlich stiel. Dazu schreiben wir im Editor links:

to stiel
setpc green fd 400
end

Dieses Programm steht uns ab sofort als neuer Befehl stiel zur Verfügung und kann nach Bedarf dazu verwendet werden, um grössere Programme zu schreiben.

3. Wir schreiben das Programm blüte:

Hier wird es erstmals etwas kniffliger. Wir stellen uns die Frage, wie man die Blüte im Bild zeichnen kann. Aus dem Aufgabentext wissen wir, dass eine Blüte aus zehn Quadraten besteht. Wir betrachten das Bild im Detail und erkennen die zehn Quadrate, aus welchen das Muster besteht:

Dank unserer vorherigen Arbeit in Schritt 1 können wir das erste Quadrat einfach zeichnen, indem wir unseren Befehl quadrat aufrufen. Die Schildkröte steht in der Mitte der Blüte und zeichnet aus dieser Position das erste Quadrat. Was nun? Offensichtlich ist das zweite Quadrat leicht rotiert gezeichnet, aber um wie viel wissen wir nicht... Was wir jedoch wissen, ist, dass alle zehn Quadrate schön regelmässig angeordnet sind und sich sozusagen einmal im Kreis drehen. Genauer gesagt ist es die Schildkröte, die sich hier einmal im Kreis dreht. Stelle dir vor, wie sich die Schildkröte mit jedem weiteren Quadrat ein bisschen weiter dreht. Am Schluss, nach dem letzten Quadrat, steht die Schildkröte wieder genau da, wo sie angefangen hat, und sie schaut auch wieder in die exakt identische Richtung (nämlich nach oben). Sie hat sich demzufolge einmal vollständig um die eigene Achse gedreht und dabei eine Drehung um 360 Grad vollzogen. Diese 360 Grad wurden gleichmässig aufgeteilt auf 10 Quadrate. Bei jeder Drehung hat sich die Schildkröte also um ein Zehntel von 360 Grad weiter gedreht – das heisst als konkret um 36 Grad.

Wir fassen diese Erkenntnis in einem Programm zusammen:

quadrat
rt 36
quadrat
rt 36
quadrat
rt 36
quadrat
rt 36
quadrat
rt 36
quadrat
rt 36
quadrat
rt 36
quadrat
rt 36
quadrat
rt 36
quadrat
rt 36

Dies lässt sich mit dem repeat-Befehl auch abgekürzt schreiben:

repeat 10 [quadrat rt 36]

Wir beobachten, dass die Blüte so schwarz eingefärbt ist, wohingegen die Blüte in unserer Aufgabe orange ist. Wir setzen also zuerst die Stiftfarbe auf orange und zeichnen anschliessend die zehn Quadrate:

setpc orange
repeat 10 [quadrat rt 36]

Wir testen es und erhalten das gewünschte Resultat:

Wir schliessen diesen Teil der Arbeit ab, indem wir dem erarbeiteten Programm den Namen blüte geben (Achtung: Die Verwendung von Umlauten wie ä, ö oder ü funktioniert erst in den neueren Versionen von XLogoOnline):

to blüte
setpc orange
repeat 10 [quadrat rt 36]
end

Dieses Programm können wir gleich mit dem Programm stiel verknüpfen, um die ganze Blume zu zeichnen...

4. Wir schreiben das Programm blume:

Nun, da es uns gelungen ist, ein Programm für den Stiel unter dem Namen stiel abzulegen und ein zweites Programm für die Blüte unter dem Namen blüte, wollen wir versuchen, die beiden Teile zu kombinieren um die gesamte Blume zu zeichnen. Ob wir zuerst mit der Blüte beginnen und dann den Stiel zeichnen, oder zuerst den Stiel und dann die Blüte, ist offen – beides ist mit ein paar leichten Anpassungen möglich. Wir haben uns hier dafür entschieden, am unteren Ende des Stiels zu beginnen und dann die Blüte oben zu platzieren.

Wir hängen die beiden Programme zusammen und sehen, was gezeichnet wird:

stiel blüte

Dies funktioniert tadellos und wir werden mit einer vollständigen Blume belohnt, so wie sie im Bild zu sehen ist:

Auch dafür legen wir einen neuen Befehl an, welchem wir den Namen blume geben wollen:

to blume
stiel blüte
end

Nun gilt es nur noch, diese Blume fünf Mal nebeneinander zu zeichnen, um eine ganze Wiese zu erhalten.

5. Wir schreiben das Programm wiese:

Um fünf Blumen nebeneinander zu platzieren, müssen wir uns zunächst nochmals bewusst werden, wie die erste Blume gezeichnet wurde: Wir haben die Blume am unteren Ende des Stiels begonnen und stehen am Ende in der Mitte der Blüte mit Ausrichtung nach oben. Um also die zweite Blume zu zeichnen, müssen wir die Schildkröte zur Startposition der zweiten Blume führen, also zu deren unterem Ende des Stiels... Dies gelingt einfach, indem wir den Stift abheben, uns nach rechts drehen und dort dann die 400 Schritte nach unten laufen, wo der nächste Stiel beginnen soll:

blume
pu
rt 90 fd 300 lt 90 bk 400
pd

Sobald dies geschafft ist, können wir die nächste Blume zeichnen:

blume
pu
rt 90 fd 300 lt 90 bk 400
pd
blume

Und wir laufen erneut zum unteren Ende der nächsten Blume:

blume
pu
rt 90 fd 300 lt 90 bk 400
pd
blume
pu
rt 90 fd 300 lt 90 bk 400
pd

Dasselbe Muster setzen wir fünf Mal fort, um alle fünf Blumen zu zeichnen:

blume
pu
rt 90 fd 300 lt 90 bk 400
pd
blume
pu
rt 90 fd 300 lt 90 bk 400
pd
blume
pu
rt 90 fd 300 lt 90 bk 400
pd
blume
pu
rt 90 fd 300 lt 90 bk 400
pd
blume
pu
rt 90 fd 300 lt 90 bk 400
pd

Oder kürzer geschrieben mit dem Befehl repeat:

repeat 5 [ blume pu rt 90 fd 300 lt 90 bk 400 pd ]

Wir sehen das erwünscht Bild...

... und speichern dieses schliesslich unter dem Namen wiese:

to wiese
repeat 5 [ blume pu rt 90 fd 300 lt 90 bk 400 pd ]
end

Zusammenfassung

Obwohl die Aufgabe auf den ersten Blick gross und komplex aussieht, gelingt es uns, die Aufgabe elegant und überschaubar zu lösen, indem wir den einzelnen Komponenten jeweils einen Namen geben, nachdem wir diese erarbeitet haben und wissen, dass die Programme das erwünschte Resultat produzieren.

Beachte: Ohne eine geplante Herangehensweise benötigt man mehrere hundert Befehle, um dieses Programm zu zeichnen. Sich dabei zu verlieren und einen Fehler zu machen, ist sehr wahrscheinlich und frustrierend. Durch unsere Herangehensweise und das Einführen neuer Befehle gelingt es uns, jeden Teil des Bildes in nur einer einzigen Programmzeile mit jeweils weniger als zehn Befehlen zu zeichnen. Das ist wesentlich einfacher zu überschauen und Fehler können viel einfacher identifiziert und behoben werden, als wenn wir keine neuen Befehle für die spezifischen Komponenten definiert hätten...

Beiträge von euch

Hier präsentieren wir ein paar ausgewählte Beiträge, die uns per E-Mail erreicht haben:

Vielen Dank für eure Teilnahme und das Einsenden eurer tollen Lösungen!

Kalenderwoche 19/20

Diese Challenge läuft von Mittwoch, dem 6. Mai 2020, bis Dienstag, dem 12. Mai 2020. Am Mittwoch, dem 13. Mai 2020, laden wir einen Lösungsvorschlag hoch.

Tutorial

Wir verwenden weiterhin die Programmierumgebung XLogoOnline (opens new window) und bearbeiten nun im Übungsheft (opens new window) die Aufgaben 23-28 (Kapitel 4, Regelmässige Vielecke und Kreise).

Übersicht

Diese Woche beschäftigen wir uns mit regelmässigen Vielecken und Kreisen. Regelmässige Vielecke zeichnen sich durch zwei Eigenschaften aus:

1. Alles Seiten sind gleich lang
2. Alle Winkel sind gleich gross

Beim Zeichnen eines Vielecks läuft die Schildkröte dessen Umfang ab und steht am Ende wieder an der ursprünglichen Startposition. Am Anfang wie am Ende ihres Wegs schaut sie in dieselbe Richtung. Der Umlauf der Schildkröte entspricht somit einer Kreisdrehung und beträgt insgesamt 360 Grad. Die Schildkröte stoppt unterwegs bei jeder Ecke und dreht sich um den gleichen Winkel. Bei einem 6-Eck stoppt sie beispielsweise 6 Mal und dreht sich jeweils um 360 : 6 = 60 Grad.

Unten siehst du ein 6-Eck abgebildet. Schaue es dir genau an und versuche, die Drehungen der Schildkröte nachzuvollziehen.

Zusammengefasst: Ein regelmässiges x-Eck besitzt x Seiten der gleichen Länge und x Ecken desselben Winkels. Wir zeichnen also x gleich lange Seiten und drehen uns dann immer um den gleichen Winkel. Unser Programm sieht folglich so aus:

repeat x [fd distanz rt 360/x]

Challenge

Auch diese Woche kannst du dich mit drei kniffligen Challenges austoben!

Tobe dich aus

Juhui, die Schule öffnet wieder ihre Tore! Freunde, Lehrer, Wandtafeln, Schultaschen und auch das z'Nüni auf dem Pausenplatz gehören bald wieder zu deinem Alltag... Worauf freust du dich am meisten? Halte einen Eindruck deines ersten Schultags als Bild fest und verwende darin mindestens vier verschiedene Vielecke.

Schick uns dein Bild und das Programm per E-Mail an weekly-challenge (at) inf.ethz.ch.

Lösung anzeigen

Challenge 1

Schritt 1

Um unsere Blume zu zeichnen, beginnen wir beispielsweise damit, dass wir ein Programm für einen blauen Blütenblatt definieren. Wir wissen, dass unser Blütenblatt ein Zehneck der Seitenlänge 50 ist. Unser Programm möchten wir möglichst kurz schreiben und verwenden aus diesem Grund den Befehl repeat:

to blattblau
repeat 10 [setpc blue fd 50 rt 360/10]
end

Schritt 2

Da unsere Blume nicht nur aus blauen Blütenblättern besteht, sondern auch aus roten Blütenblättern, schreiben wir auch für diese ein eigenes Programm:

to blattrot
repeat 10 [setpc red fd 50 rt 360/10]
end

Schritt 3

Nun haben wir zwei unterschiedliche Programmen für die beiden Blütenfarben Blau und Rot. Im dritten Schritt sollen diese beiden Programme vereint werden, damit sie am Schluss die ganze Blume zeichnen. Wir betrachten nochmals die Blume und stellen fest, dass sie aus insgesamt 6 Blütenblättern besteht. Wenn wir sie noch genauer betrachten, stellen wir fest, dass sich das Muster blau / rot bei der Reihenfolgen der Blütenblätter 3 Mal wiederholt:

Konkret bedeutet dies für unser Programm, dass unsere Schildkröte sich 3 Mal drehen muss (repeat 3), um alle 6 Blütenblätter zu zeichnen. Wichtig ist aber festzustellen, dass es 6 Blütenblätter sind und somit dreht sie sich um den Winkel rt 360/6 beziehungsweise rt 60:

to blume
repeat 3 [blattrot rt 60 blattblau rt 60]
end

Wenn wir dieses Programm ausführen, erhalten wir das folgende Bild und unsere Schildkröte befindet sich in ihrer Startposition:

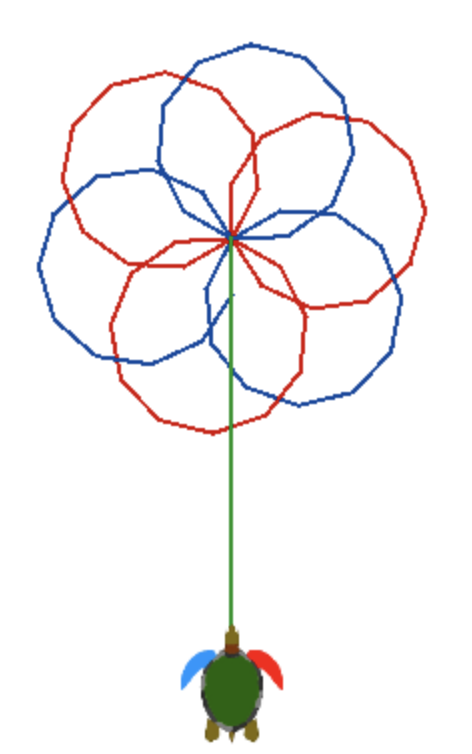
Es fällt auf, dass der Stiel der Blume noch fehlt. Wir achten auf die Position der Schildkröte und ergänzen das Programm:

to blume 
repeat 3 [blattrot rt 60 blattblau rt 60] setpc green bk 400

Challenge 2

Wie du schon weisst, gibt es immer mehr als einen Weg, ein Problem (eine Aufgabe) zu lösen. Hier ist der einfachste Lösungsweg, ein Programm für das "linke" und ein anderes für das "rechte" Dreieck zu schreiben. Was bedeutet ein linkes und ein rechtes Dreieck?

Nun, ein rechtes Dreieck zeichnen wir auf folgende Weise:

fd 100 rt 120
fd 100 rt 120 
fd 100 rt 120

Oder kürzer:

repeat 3 [fd 100 rt 120]

Wir definieren jetzt einen neuen Befehl dreieckr im Editor, der ein Dreieck wie das im Bild dargestellte zeichnet:

to dreieckr
repeat 3 [fd 100 rt 90]
end 

Um ein sogenanntes linkes Dreieck zu zeichnen, sollte die Schildkröte immer eine Linksdrehung ausführen:

fd 100 lt 120     
fd 100 lt 120 
fd 100 lt 120

Oder kürzer:

repeat 3 [fd 100  lt 120]

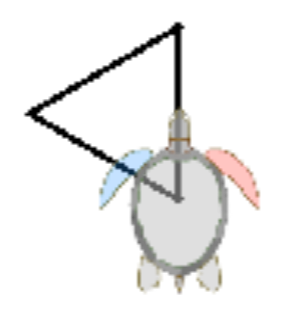
Auch hier können wir einen neuen Befehl im Editor definieren:

to dreieckl
repeat 3 [fd 100 rt 90]
end

Jetzt können wir den Befehl dreieckr verwenden, um eine Spalte mit vier Dreiecken zu zeichnen, die alle nach rechts zeigen. Hier ist es wichtig zu beachten, dass wir den Befehl dreieckr, der nichts anderes als ein Programm selbst ist, innerhalb eines anderen Programms namens spalte4 aufrufen können:

to spalte4
repeat 4 [dreieckr fd 100]
end

Der nächste Schritt besteht darin, die Schildkröte so zu positionieren, wie es für das Zeichnen der Säule aus drei Dreiecken sinnvoll ist. Aber um die bereits vorhandenen Linien nicht zu wiederholen, ist es besser, die linken Dreiecke zu verwenden. Die Neupositionierung erfolgt durch:

rt 120 fd 100 rt 60

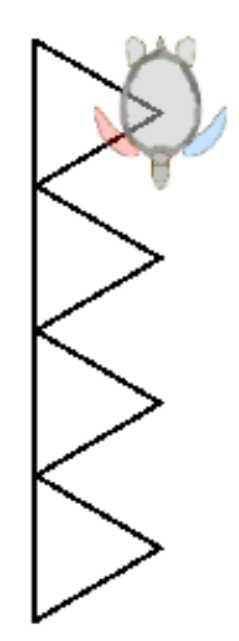
Als nächstes muss das Programm für die Spalte der drei linken Dreiecke geschrieben werden:

to spalte3
repeat 3 [dreieckl fd 100]
end

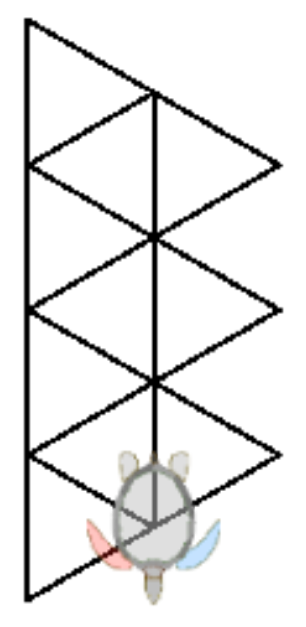
Und die Schildkröte neu zu positionieren:

lt 120 fd 100 lt 60

Als nächstes muss das Programm für die Spalte der zwei rechten Dreiecke geschrieben werden:

to spalte2
repeat 2 [dreieckr fd 100]
end

Mit der Neupositionierung der Schildkröte und dem Zeichnen des allerletzten linken Dreiecks haben wir unsere Aufgabe erfüllt:

rt 120 fd 100 rt 60

Der Befehl dreieckl erledigt die Aufgabe.

Übersicht über Unterprogramme – neu definierte Befehle zusammengefasst:

to dreieckr
repeat 3 [fd 100 rt 120]
end 

to dreieckl
repeat 3 [fd 100 lt 120]
end 

to spalte4
repeat 4 [dreieckr fd 100]
end

to spalte3
repeat 3 [dreieckl fd 100]
end

to spalte2
repeat 2 [dreieckr fd 100]
end

Und schliesslich das Programm, das die entsprechenden Unterprogramme aufruft und das Bild zeichnet:

to image
spalte4
rt 120 fd 100 rt 60
spalte3
lt 120 fd 100 lt 60
spalte2
rt 120 fd 100 rt 60
dreieckl
end

Challenge 3: Die Trauminsel

In dieser Aufgabe wollen wir eine Insel mit drei Palmen zeichnen. Wir bearbeiten die Aufgabe in drei Schritten: Zunächst befassen wir uns mit dem Zeichnen einer Palme und erstellen dazu einen neuen Befehl. Dann kümmern wir uns darum, die Insel zu zeichnen und die Palmen darauf anzuordnen. Zuletzt ergänzen wir das Bild mit dem blauen Meeresspiegel:

1. Palme zeichnen und einen neuen Befehl dafür anlegen.

Wir zeichnen zunächst die Palme und starten das Bild am unteren Ende des Stammes. Der Stamm ist eine braune Linie der Länge 100, welche wir mit den Befehlen setpc brown fd 100 zeichnen können. Oben angekommen setzen wir die Stiftfarbe auf grün, um anschliessend die Palmenblätter zu zeichnen. Insgesamt erhalten wir das folgende Programm:

setpc brown
fd 100
setpc green

Ein einzelnes Palmenblatt zu zeichnen, stellt keine grosse Schwierigkeit dar:

fd 50 bk 50

Aber um nun 20 solche Blätter in einem Kreis anzuordnen, müssen wir die Schildkröte nach jedem Blatt ein wenig drehen.

repeat 20 [ fd 50 bk 50 rt ??? ]

Ähnlich wie bei Vielecken dreht sich die Schildkröte auch hier einmal um die eigene Achse und somit um 360 Grad. Unterwegs stoppt sie 20 Mal. Sie zeichnet jeweils ein Blatt und dreht sich ein wenig. Um die Blätter regelmässig anzuordnen, drehen wir die Schildkröte also bei jedem Zwischenstopp um ein Zwanzigstel von 360 Grad. So steht die Schildkröte nach 20 Stopps nämlich genau wieder so wie am Anfang:

repeat 20 [ fd 50 bk 50 rt 360/20 ]

Wir setzen die beiden Teile zusammen:

setpc brown
fd 100
setpc green
repeat 20 [ fd 50 bk 50 rt 360/20 ]

Am Schluss führen wir die Schildkröte wieder zurück zum Anfang des Stammes mit den Befehlen setpc brown bk 100 und wir fassen alle Teile in einem eigenen Programm zusammen unter dem Namen palme:

to palme
  setpc brown 
  fd 100 
  setpc green
  repeat 20 [ fd 50 bk 50 rt 360/20 ]
  setpc brown
  bk 100
end

2. Insel zeichnen und Palmen darauf anordnen

Die Insel (ohne Palmen) ist ein Halbkreis mit Schrittgrösse 1 - man könnte das also relativ einfach zeichnen mit den Befehlen repeat 180 [fd 1 rt 1]. Allerdings stellt sich bald die Frage, wie man dann die drei Palmen auf der Insel anordnen soll. Wir konzentrieren uns hier darauf, die kleinen Inselsegmente zwischen den Palmen zu zeichnen.

Offensichtlich sind die Palmen regelmässig auf der Insel angeordnet, also mit regelmässigen Abständen zwischen ihnen. Die Palmen unterteilen die Insel in 8 Segmente, die im Bild unten dargestellt sind:

Wie zeichnet man einen Achtelkreis? Lass uns bei einem ganzen Kreis beginnen und die Seiten immer weiter einschränken:

#Kreis:
repeat 360 [fd 1 rt 1]

#Halbkreis:
repeat 180 [fd 1 rt 1]

#Vertelkreis:
repeat 90 [fd 1 rt 1]

#Achtelkreis:
repeat 45 [fd 1 rt 1]

Auch das speichern wir wieder in einem Befehl ab, diesmal mit dem Namen segment:

to segment
setpc brown
repeat 45 [fd 1 rt 1]
end

Nun ist es nicht mehr allzu schwierig, die gesamte Insel zu zeichnen. Dazu zeichnen wir immer abwechselnd ein Inselsegment und anschliessend eine Palme:

segment
lt 90 palme rt 90

segment
lt 90 palme rt 90

segment
lt 90 palme rt 90

segment

Das einzige, was nun noch fehlt, ist das Meer.

3. Meer zeichnen.

Wir wissen, dass das Meer eine blaue Linie der Länge 500 ist. Die Linie sieht einigermassen zentriert aus, wir wissen allerdings nicht, wie breit die Insel ist. Also experimentieren wir mit verschiedenen Werten. Eine Strategie, die passend erscheint, ist, dass man zunächt um 200 Schritte von der Insel nach rechts läuft, um anschliessend die 500 Schritte rückwärts zu gehen:

segment
lt 90 palme rt 90

segment
lt 90 palme rt 90

segment
lt 90 palme rt 90

segment
lt 90 setpc blue fd 200 bk 500

Beiträge von euch

Hier präsentieren wir ein paar ausgewählte Beiträge, die uns per E-Mail erreicht haben:

Vielen Dank für eure Teilnahme und das Einsenden eurer tollen Lösungen!

Kalenderwoche 20/21

Diese Challenge läuft von Mittwoch, dem 13. Mai 2020, bis Dienstag, dem 19. Mai 2020. Am Mittwoch, dem 20. Mai 2020, laden wir einen Lösungsvorschlag hoch.

Tutorial

Wir verwenden weiterhin die Programmierumgebung XLogoOnline (opens new window) und bearbeiten nun im Übungsheft (opens new window) die Aufgaben 29-34 (Kapitel 5, Programme mit Parametern).

Übersicht

Viele Befehle, die du bisher gelernt hast (beispielsweise fd 100), bestehen aus zwei Teilen:

Befehlsname (z.B. fd) und Parameter (z.B. 100). Die Programme, die du bisher geschrieben hast, enthielten Parameter um Seitenlängen, Winkelgrössen und Farben anzugeben.

Diese Woche lernst du Programme zu schreiben, mit denen du Eigenschaften wie Seitenlängen, Winkelgrössen und Farben beim Aufruf des Programmes frei wählen kannst. Dadurch können wir Tausende von verschiedenen Mustern in nur einem einzigen Programm beschreiben.

Betrachten wir das folgende Beispiel:

Alle Programme quadratA bis quadratF sehen fast gleich aus. Der einzige Unterschied liegt jeweils beim Parameterwert des Befehls fd (der Wert ist einmal 50, einmal 75, einmal 150, einmal 250, einmal 300 und einmal 400). Die Idee ist nun, all diese Programme zu einem einzigen Programm zusammenzufassen, in welchem wir keinen Parameterwert für den Befehl fd angeben. Wir stellen uns den Wert erstmal als leere Stelle vor, die erst beim Aufrufen des Programms festgelegt wird. Es ist aber wichtig, die leere Stelle zu benennen. Dafür wählen wir in diesem Fall den Namen :seitenlaenge (Achtung! Der Doppelpunkt ist zwingend nötig).

Unser Programm sieht nun so aus:

Nachdem du das Programm im Editor geschrieben hast, kannst du es im Eingabefeld eingeben und dahinter eine beliebige Zahl schreiben. Schon zeichnet die Schildkröte ein Quadrat in der von dir gewählten Grösse.

Beachte: Zwischen dem Befehlsnamen quadrat und dem Parameterwert (z.B. 50) muss jeweils ein Abstand stehen.

Challenge

Auch diese Woche erwarten dich wieder drei knifflige Challenges:

Tobe dich aus

Du magst durchgedrehte Ideen? Wir auch! 😄 Gestalte dein eigenes total durchgedrehtes Fortbewegungsmittel. Ein Kamel mit 4 Höckern? Rollschuhe mit 16 Rädern? Eine Limousine mit 38 Türen? Klar, wieso nicht?! Schreibe dein Programm mit einem Parameter, so dass wir alle möglichen Varianten deines durchgedrehten Fortbewegungsmittels zeichnen können.

Schick uns dein Bild und das Programm per E-Mail an weekly-challenge (at) inf.ethz.ch.

Lösung anzeigen

• Challenge A: Die unendliche Leiter

Schritt 1

Zunächst überlegen wir uns, mit welchem Programm wir eine einzelne Sprosse zeichnen können. Wie immer müssen wir uns dazu Gedanken machen, wo unsere Schildkröte beim Start platziert sein soll und an welcher Stelle sie sich am Ende des Programms befinden soll.

In diesem Fall entscheiden wir uns, die Schildkröte unten links zu platzieren (siehe Bild).

Wir schreiben das folgende Programm um die Sprosse zu zeichnen:

fd 100 bk 50 rt 90 fd 100 lt 90 fd 50 bk 100

und erhalten das folgende Bild:

Schritt 2

Nun überlegen wir uns, wo die Schildkröte am Ende des Programms am besten platziert sein soll. Weil die Endposition das sofortige Zeichnen einer nächsten Sprosse mit dem gleichen Programm ermöglichen soll, entscheiden wir uns dafür, die Schildkröte in der Mitte links zu platzieren. Aus diesem Grund ergänzen wir das bereits angefangene Programm wie folgt:

fd 100 bk 50 rt 90 fd 100 lt 90 fd 50 bk 100 fd 50 rt 90 bk 100 lt 90

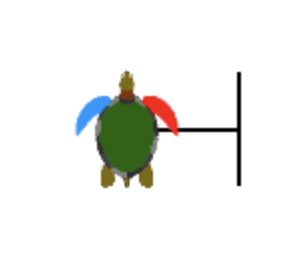
Schritt 3

Nun geht es darum, ein Programm zu schreiben und zu benennen, das uns ermöglicht, Leitern mit beliebig vielen Sprossen zu zeichnen. Dafür setzen wir sowohl das neu erlernte Konzept des Parameters ein, als auch das altbekannte repeat. Wir nennen das Programm leiter und in derselben Zeile schreiben wir auch :sprossen. :sprossen stellt den Parameter in diesem Programm dar und ermöglicht uns, beliebig viele Sprossen bei einer Leiter auszuwählen, abhängig davon, welche Zahl wir angeben. Weiter setzen wir im Programm auch repeat ein, denn bis jetzt haben wir nur ein Programm für eine einzelne Sprosse geschrieben. Weil repeat immer mit einer Anzahl an Wiederholungen einher geht, wir aber kurzfristig entscheiden wollen, wie viele Sprossen wir bei den Leitern haben möchten, setzen wir bei repeat ebenfalls :sprossen als Parameter ein. Unter Berücksichtigung all dieser Bedingungen schreiben wir das folgende Programm:

to leiter :sprossen
repeat :sprossen [fd 100 bk 50 rt 90 fd 100 lt 90 fd 50 bk 100 fd 50 rt 90 bk 100 lt 90 ]
end

Wenn wir nun beispielsweise leiter 6 in der Befehlseingabe eingeben, erhalten wir die folgende Leiter mit 6 Sprossen:

• Challenge B: Quadrat im Quadrat im...

Das Bild, das wir zeichnen wollen, besteht aus Quadraten, die ein ganz bestimmtes Seitenlängenverhältnis haben. Die Seite jedes grösseren Quadrats ist doppelt so gross wie die Seite des nächstgelegenen kleineren Quadrats.

Wie du schon weisst, kann man ein Quadrat beliebiger Grösse einfach mit einem neudefinierten Befehl zeichnen:

to quadrat :l
repeat 4 [fd :l rt 90]
end 

Beginnen wir mit dem kleinsten Quadrat, das eine Seitenlänge von 100 Schritten hat. Wir können einfach in das Eingabefeld tippen: quadrat 100 und wir haben es. Aber wir möchten die Schildkröte nach dem Zeichnen richtig positionieren, sodass wir das nächstgrössere Quadrat einfach zeichnen können. Dieses ist 200 x 200 Schritten gross. Wenn wir jede Seite des kleinsten Quadrats um 50 Schritte (100:2) auf beiden Enden verlängern, erhalten wir ein Quadrat mit einer Seitenlänge von 200 Schritten, das richtig zentriert ist. Und um die Schildkröte zu positionieren, ohne eine Linie zu zeichnen, verwenden wir die Befehle pu und pd. Das Programm sieht jetzt so aus:

to quadpos :l
repeat 4 [fd :l rt 90]
pu bk :l/2 rt 90 bk :l/2 lt 90 pd
end

Wenn wir quadpos 100 in das Eingabefeld eintragen und "Enter" drücken, erhalten wir das folgende Bild:

Alles, was wir jetzt noch tun müssen, ist das Quadrat 200 x 200 zu zeichnen. Das Programm für Quadrate beliebiger Grosse mit dem Ausrichten der Schildkröte haben wir schon: quadpos :l. Statt :l schreiben wir 200. Das nächstgrössere Quadrat beträgt 400 x 400 Schritte. Das bedeutet, dass wir an jeder Seite des 200 x 200 Quadrats an beiden Enden 100 Schritte (200 : 2) weiterlaufen müssen. Um das Quadrat 400 x 400 zu zeichnen, schreibst du: quadpos 400. Und als letzten Schritt, für das Quadrat 800 x 800, schreibst du quadpos 800. Du kannst so weiter beliebig viele Quadrate zeichnen, nur vergiss jeweils nicht, die Seite zu verdoppeln.

to quad_alle
quadpos 100
quadpos 200
quadpos 400
quadpos 800
end 

• Challenge C: Ein Quadrat von Kreisen

In dieser Aufgabe zeichnen wir Quadrate, die aus farbigen Kreisen bestehen. Wir schauen uns die Lösung in mehreren Schritten an. Zunächst wollen wir nur das Muster zeichnen; erst in einem weiteren Schritt kümmern wir uns darum, das Programm zu parametrisieren. Für den Anfang konzentrieren wir uns nur darauf, exakt das folgende Muster zu zeichen:

Die Anzahl der Kreise pro Seite setzen wir zunächst fix auf 5 und die Farbe auf Schwarz.

In den folgenden Schritten werden wir zunächst (a) einen einzelnen Kreis zeichnen, (b) mehrere Kreise zu einer Seite zusammensetzen, (c) mehrere Seiten zu einem vollständigen Quadrat zusammenführen und (d) das ganze Programm parametrisieren.

1. Kreis zeichnen

Seit einiger Zeit wissen wir, wie man einen Kreis als 360-Eck zeichnen kann. Wir starten den Kreis an dessen linken Seite und laufen anschliessend 360 kleine Schritte, nach welchen wir uns immer um genau 1 Grad nach rechts drehen. Am Schluss stehen wir wieder an derselben Stelle wie am Anfnag und haben uns unterwegs um 360 Grad gedreht:

repeat 360 [fd 1 rt 1]

2. Eine Seite des Quadrats zeichnen

Als nächstes wollen wir fünf solche Kreise nebeneinander legen um damit eine Seite unseres Quadrats zu zeichnen (beispielsweise die obere Seite des Quadrats):

Eine Seite besteht aus 5 Kreisen. Nachdem wir den ersten Kreis gezeichnet haben, laufen wir zur Startposition des zweiten Kreises. In diesem Fall befindet sich die Startposition auf der gegenüberliegenden rechten Seite des Kreises. Wir zeichnen also einen Halbkreis:

repeat 360  [fd 1 rt 1]
repeat 180 [fd 1 rt 1]

Die beiden Programme können zusammengefasst werden zu einem einzigen Programm, welches direkt eineinhalb Kreise zeichnet. Dazu addieren wir 360 + 180, da das erste Programm 360 Wiederholungen der Befehle fd 1 rt 1 macht, während das zweite Programm 180 Wiederholungen derselben beiden Befehle fd 1 rt 1 macht. Eineinhalb Kreisumdrehungen zeichnen wir also wie folgt:

repeat 540 [fd 1 rt 1] 

Wir geben dem Programm den Namen eineinhalbkreise, um es in Zukunft einfach aufrufen zu können:

to eineinhalbkreise
repeat 540 [fd 1 rt 1]
end

Nach eineinhalb Umdrehungen steht die Schildkröte kopfüber. Das ist nicht geschickt, wenn wir den zweiten Kreis zeichnen wollen, denn dann sollte die Schildkröte (wie zu Beginn) nach oben schauen. Wir drehen sie also um 180 Grad, sodass sie wieder nach oben guckt:

eineinhalbkreise
rt 180

Ab diesem Moment sind wir bereit, mehrere Kreise zu zeichnen. Das folgende Programm zeichnet alle fünf Kreise einer Seite:

# Fünf Kreise:
repeat 5 [eineinhalbkreise rt 180]

Hinweis: Angenommen, wir wollten hier nur zwei, drei oder vier Kreise haben, so müssten wir das Programm wie folgt anpassen. (Diese Beobachtung wird in Schritt 4 wichtig.)

# Zwei Kreise:
repeat 2 [eineinhalbkreise rt 180]

# Drei Kreise:
repeat 3 [eineinhalbkreise rt 180]

# Vier Kreise:
repeat 4 [eineinhalbkreise rt 180]

3. Ein Quadrat zeichnen

Als nächstes wollen wir uns damit beschäftigen, wie man vier Seiten (bestehend aus mehreren Kreisen) zu einem Quadrat kombinieren kann. Wir wissen bereits, wie man eine einzelne Seite zeichnet. Nun stellt sich die Frage, wie man die Schildkröte ausrichten muss, nachdem die erste Seite gezeichnet ist. Wir erinnern uns: Am Anfang hat die Schildkröte auf der linken Seite des ersten Kreises (links) begonnen und von dort die restlichen Kreise rechts gezeichnet. Derselbe Punkt liegt also bei der zweiten Seite des Quadrats an der folgenden Stelle:

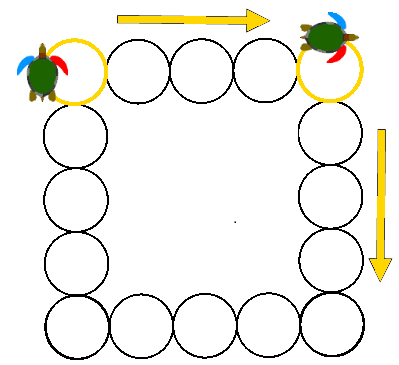
Wir wissen, wo wir hin wollen. Aber wo steht die Schildkröte denn momentan eigentlich? Nachdem eine vollständige erste Seite gezeichnet wurde, befindet sich die Schildkröte auf der rechten Seite des Kreises ganz rechts und schaut nach oben. Zwischen den beiden Punkten liegt ein Viertelkreis nach links, welchen wir wir folgt programmieren können:

repeat 90 [fd 1 lt 1] 

Wir benennen das Programm viertelkreis, um spätere Aufrufe zu vereinfachen:

to viertelkreis
repeat 90 [fd 1 lt 1]
end

Anschliessend müssen wir die Schildkröte wieder korrekt ausrichten, sodass sie in ihrer neuen Position wieder in derselben Ausgangslange ist wie am Anfang:

repeat 5 [eineinhalbkreise rt 180]
viertelkreis
rt 180

Diese drei Teile können nun mehrmals wiederholt werden, um die vier Seiten des Quadrats zu zeichnen:

repeat 4 [repeat 5 [ eineinhalbkreise rt 180] viertelkreis  rt 180]

Wir verpacken das Programm in einem Befehl kreise so wie in der Aufgabenstellung vorgeschlagen:

to kreise 
repeat 4 [repeat 5 [eineinhalbkreise rt 180] viertelkreis  rt 180]
end

4. Parametrisieren

Der letzte Schritt liegt nun noch darin, das Muster zu parametrisieren. Zwei Punkte sollen parametrisiert werden, nämlich:

• Die Anzahl der Kreise pro Seite
• Die Farbe des Musters insgesamt

In einem vorherigen Schritt haben wir bereits festgehalten, dass die Zahl 5 im Programm repeat 5 [eineinhalbkreise rt 180] angibt, wie viele Kreise eine Seite des Quadrats enthalten wird. Wenn man also Quadrate verschiedener Seitenlänge zeichnen will, muss nur diese Zahl angepasst werden. Im folgenden Code siehst du einige Beispiele verschiedener Quadrate:

to kreiseA
repeat 4 [repeat 2 [eineinhalbkreise rt 180] viertelkreis  rt 180]
end

to kreiseB
repeat 4 [repeat 3 [eineinhalbkreise rt 180] viertelkreis  rt 180]
end

to kreiseC
repeat 4 [repeat 3 [eineinhalbkreise rt 180] viertelkreis  rt 180]
end

Um alle Programme in einem einzigen Programm zu vereinigen, ersetzen wir diesen Wert mit einem Platzhalter :anz:

to kreise :anz
repeat 4 [repeat :anz [eineinhalbkreise rt 180] viertelkreis  rt 180]
end

Dieses Programm kann nun aufgerufen werden und führt bereits dazu, dass wir beliebig grosse Quadrate zeichnen können, indem wir den Parameter entsprechend wählen (kreise 2, kreise 3, kreise 4 zeichnen beispielsweise die Muster, welche wir zuvor gesehen haben).

Die nächste Frage befasst sich mit der Farbe unseres Musters. Bisher war das Muster schwarz. Es gelingt uns einfach, das Muster in einer bestimmten Farbe zu zeichnen, indem wir zu Beginn den Befehl setpc verwenden. Die folgende Erweiterung führt beispielsweise dazu, dass das Muster immer in rot gezeichnet wird:

to kreise :anz
setpc red
repeat 4 [repeat :anz [eineinhalbkreise rt 180] viertelkreis  rt 180]
end

Wir wollen allerdings nicht immer die Farbe Rot. Dieser Wert soll von Fall zu Fall angepasst werden können. Wir parametrisieren also auch die Farbe nach dem Befehl setpc und führen dazu einen zweiten Platzhalter :farbe ein:

to kreise :anz :farbe
setpc :farbe
repeat 4 [repeat :anz [eineinhalbkreise rt 180] viertelkreis  rt 180]
end

Nun können sowohl die Grösse des Quadrats, als auch die Farbe des Musters beim Start gewählt werden. Wir testen die beiden Beispiele aus der Aufgabenstellung (kreise 3 red und kreise 2 yellow) und sehen das erwünschte Resultat.

Achtung: Diese Aufgabe verwendet mehrere Parameter. In diesem Falle ist es wichtig, die Reihenfolge der Parameter zu beachten. Wenn unser Programm im Editor kreise :anz :farbe heisst, so wird der erste Wert als die Anzahl der Kreise verstanden und der zweite Wert wird als die zu verwendende Farbe benutzt. Verwechselt man aus Versehen die Reihenfolge beim Aufrufen des Programms (beispielsweise so: kreise red 3), so würde der Wert red irrtümlicherweise nach repeat platziert und der Wert 3 würde nach dem Befehl setpc eingesetzt. Dies kann zu seltsamen Fehlern führen und es lohnt sich, diese Reihenfolge im Hinterkopf zu behalten und zu kontrollieren.

Beiträge von euch

Hier präsentieren wir ein paar ausgewählte Beiträge, die uns per E-Mail erreicht haben:

Vielen Dank für eure Teilnahme und das Einsenden eurer tollen Lösungen!

Kalenderwoche 21/22

Diese Challenge läuft von Mittwoch, dem 20. Mai 2020, bis Dienstag, dem 26. Mai 2020. Am Mittwoch, dem 27. Mai 2020, laden wir einen Lösungsvorschlag hoch.

Tutorial

Wir verwenden weiterhin die Programmierumgebung XLogoOnline (opens new window) und bearbeiten nun im Übungsheft (opens new window) die Aufgaben 61-70 (Kapitel 6, Blumen zeichnen und Parameter an Unterprogramme übergeben).

Übersicht

Wir sind in der letzten Woche unserer Programmier-Challenge angelangt. Bisher hast du gelernt, wie du grosse und komplexe Bilder mit Unterprogrammen einfacher zeichnen kannst. Du hast auch gelernt, Programme mit Parametern zu schreiben, die Tausende von Bildern zaubern können. Diese Woche wollen wir diese zwei Punkte verbinden und uns damit beschäftigen, wie man Parameter an Unterprogramme übergibt.

Lass uns beispielsweise ein paar Häuser zeichnen...

Schritt 1: Dreiecke und Quadrate zeichnen

Du weisst bereits, wie du Dreiecke und Quadrate beliebiger Grösse zeichnen kannst:

to quadrat :gr
  repeat 4 [fd :gr rt 90]
end

to dreieck :gr
  lt 90
  repeat 3 [fd :gr lt 120]
end

Damit kreieren wir nun bequem Quadrate und Dreiecke aller Grössen:

Schritt 2: Dreiecke und Quadrate zu Häusern zusammen setzen

Aus den zwei Programmen lassen sich nun Häuser zeichnen. Dazu kombinieren wir je ein Quadrat und ein Dreieck derselben Grösse. Wir zeichnen drei verschiedene Häuser:

to hausA
  quadrat 100
  fd 100
  dreieck 100
end

to hausB
  quadrat 200
  fd 200
  dreieck 200
end

to hausC
  quadrat 300
  fd 300
  dreieck 300
end

Die drei Programme zeichnen je eines der folgenden drei Häuser:

Schritt 3: Aus drei mach eins (Programme kombinieren)

Wenn wir die drei Programme hausA, hausB und hausC vergleichen, bemerken wir, dass sich diese jeweils nur durch drei Parameterwerte unterscheiden, der Rest bleibt über alle drei Programme gleich. Wir kombinieren also alle drei Programme zu einem und ersetzen dabei die veränderlichen Teile durch einen Parameter :gr (um die Grösse des Hauses anzugeben):

to haus :gr
  quadrat :gr
  fd :gr
  dreieck :gr
end

Um mit diesem Programm ein Haus zu zeichnen, rufen wir das neue Programm auf und wählen einen passenden Parameterwert (zum Beispiel haus 100). Dabei wird der gewählte Wert zunächst an das Programm haus übergeben, wo er den Platzhalter :gr mit dem Wert 100 füllt. Anschliessend werden die Unterprogramme quadrat, fd und dreieck ausgeführt. Auch diese verwenden den Wert :gr und so wird der Wert 100 auch an die drei Unterprogramme geschickt. Dort wird er verwendet, um die verschiedenen Teile des Hauses zu zeichnen, wie im folgenden Diagramm dargestellt:

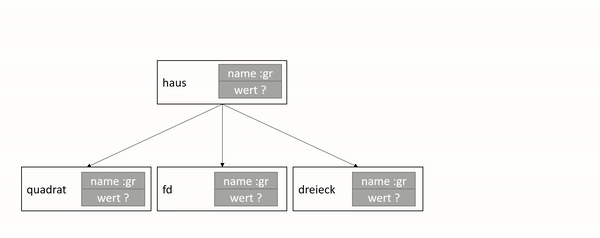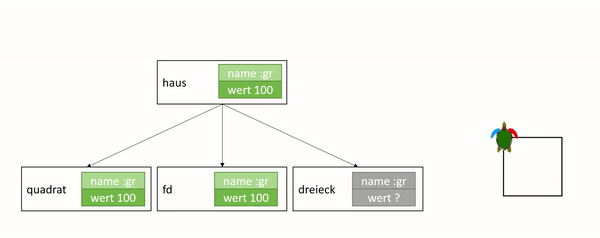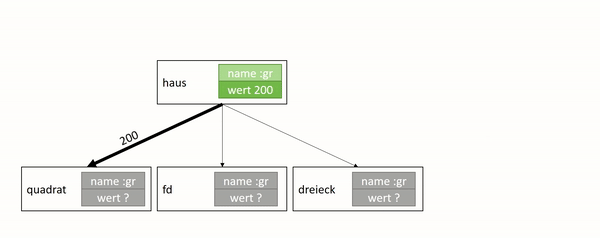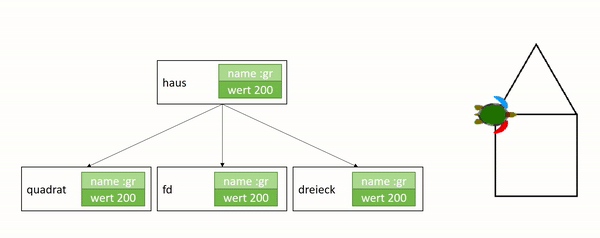
Challenge

Auch diese Woche erwarten dich wieder drei knifflige Challenges:

Tobe dich aus

In den letzten acht Wochen hast du richtig viel übers Programmieren mit LOGO gelernt. Als "Grande Finale" kombinieren wir alles, was du bisher gelernt hast. Lass deiner Phantasie freien Lauf und überrasche uns mit einem grossen, bunten und besonders schönen Feuerwerk!

Schick uns dein Bild und das Programm per E-Mail an weekly-challenge (at) inf.ethz.ch.

Lösung anzeigen

Challenge 1 - Färbe das Muster

In dieser Aufgabe hast du die beiden Programmen, muster und kreis mit Parametern erweitert. Im Folgenden schauen wir uns gemeinsam einen möglichen Weg an, der die Aufgabe in 4 Schritten löst.

• Schritt 1:

Wir beginnen damit, dass wir ein Programm für einen Kreis schreiben. Es gibt zwei Möglichkeiten: Entweder der Kreis wird nach rechts gezeichnet oder er wird nach links gezeichnet. Das führt zu unterschiedlichen Startpositionen, einmal beginnt man links und läuft im Uhrzeigersinn um den Kreis herum - oder man beginnt rechts und läuft im Gegenuhrzeigersinn um den Kreis herum. Mit einem Blick auf die Startposition im Bild entscheiden wir uns, den Kreis links zu beginnen und im Uhrzeigersinn abzulaufen. Wir nennen unser Programm kreis und entscheiden uns ausserdem dafür, einen Kreis mit einem Umfang von 360 Schritten als Grösse zu nehmen (das heisst also 360 kleine Schritte der Grösse 1). Unser Programm für einen Kreis sieht folglich so aus:

to kreis
repeat 360 [fd 1 rt 1]
end

Dieses Programm zeichnet einen Kreis. Fällt dir aber etwas auf? Genau! Wir wollen die Farbe des Kreises bestimmen können und möchten dafür einen Parameter einsetzen. Zu diesem Zweck passen wir das Programm auf die folgende Weise an:

to kreis :farbekreis
setpc :farbekreis
repeat 360 [fd 1 rt 1]
end

Wenn du nun beispielsweise kreis red in der Eingabezeile eingibst, erscheint ein roter Kreis. Dasselbe funktioniert für alle möglichen Farben.

• Schritt 2

Nun möchten wir das in der Aufgabenstellung vorgegebene Programm muster etwas anpassen. Schaue dir das vorgegebene Programm und die Bilder in der Aufgabe kurz an:

to muster 
repeat 4 [kreis fd 100 lt 90 fd 100]
end

Was denkst du, fehlt hier? Ganz genau! Die zwei Parameter, die die Kreisfarbe und die Farbe des Quadrats bestimmen. Ein guter Teil der Arbeit ist schon erledigt - wir wissen, wie man einen farbigen Kreis zeichnen kann. Aber wie verwendet man den Befehl kreis nun im Programm muster?

Wir schreiben das Programm erneut und fügen die zwei Parameter :farbekreis und :farbequadrat ein:

to muster :farbekreis :farbequadrat
repeat 4 [kreis :farbekreis setpc :farbequadrat fd 100 lt 90 fd 100]
end

Wir zeichnen also zuerst einen Kreis in einer gewissen Farbe, wechseln dann den Stift zu einer anderen Farbe und zeichnen zuletzt eine Seite des Quadrats. Wenn man diese paar einfachen Befehle viermal nacheinander ausführen lässt, sehen wir ein gefärbtes Quadrat mit Kreisen. Toll!

• Schritt 3:

Die beiden Bilder in der Aufgabenstellung können nun bequem und einfach aufgerufen werden mit unserem neuen Befehl muster:

muster brown green

mutser black red

Teste eines der beiden Programme in der Eingabezeile und schon siehst du eines der folgenden zwei Bilder aus der Aufgabenstellung:

Mit den beiden Parametern kannst du natürlich auch viele andere Bilder zeichnen, setze dazu einfach zwei beliebige Farben deiner Wahl als Parameter ein...

Challenge 2 - Der Frühling kommt!

Unsere schönen Blumen bestehen aus Sechsecken. Deshalb beginnen wir mit dem Unterprogramm sechseck :l :f, welches ein beliebig grosses Sechseck in einer beliebigen Farbe zeichnet. Die Grösse des Sechsecks wird durch die Länge der Seite definiert. Im Unterprogrammm sechseck :l :f wird der Parameter :l für die Länge der Seite und der Parameter :f für die Farbe verwendet.

to sechseck :l :f
setpc :f
repeat 6 [fd :l lt 60 ]
end

Wir können einfach überprüfen, ob das Unterpogramm sechseck :l :f funktioniert und zeichnen ein pinkes, ein blaues und ein gelbes Sechseck. In diesem Beispiel betragen die Seiten des Sechsecke 50 Schritte.

Im nächsten Schritt schreiben wir das Unterprogramm, mit dem die Blume aus sechs Sechsecken gezeichnet wird.

to blume :l :f
repeat 6 [sechseck :l :f
fd :l rt 60]
end

Um das Programm zu testen, schreiben wir im Eingabefeld: blume 50 blau.

Wir müssen in der Mitte noch ein gelbes Sechseck zeichnen. Dazu fügen wir im Unterprogramm blueme :l :f noch einige Befehle hinzu. Zu diesen Befehlen gehört die Neupositionierung der Schildkröte, indem sie um 120 Grad nach rechts gedreht wird, und das Unterprogram, das gelbe Sechseck zeichnet.

Hier ist es sehr wichtig zu beachten, dass das Unterprogramm für das gelbe Sechseck einen "freien" Parameter und einen bestimmten Parameter hat. Der "freie" Parameter ist für die Seitenlänge des Sechsecks, die wir wählen können. Der andere Parameter ist als die Farbe "yellow" (Gelb) definiert. Deswegen rufen wir im Unterprogramm sechseck :l yellow auf. Das Unterporgram blume :l :f sieht jetzt so aus:

to blume :l :f
repeat 6 [sechseck :l :f
fd :l rt 60]
rt 120 sechseck :l yellow
end

Bei der Eingabe von blume 50 blue im Eingabefeld zeichnet die Schildkröte Folgendes:

Unser Strauss besteht aus sechs Blumen, die sich in ihrer Farbe abwechseln. Eine Möglichkeit ist es, ein Unterprogramm zu schreiben, das nur Blumen in einer Farbe zeichnet. Zum Beispiel:

to blume3 :l :f
repeat 3[setpc green fd :l*4 lt 60 
blume :l :f lt 60 
setpc green bk :l*4 rt 120]
end

Bei der Eingabe von blume3 50 blue im Eingabefeld zeichnet die Schildkröte nun Folgendes:

Beim der Eingabe von blume3 50 pink im Eingabefeld erhalten wir:

Alles, was wir machen müssen, ist die blaue oder pinke Blume um 60 Grad zu drehen. Schreiben wir jetzt das Programm strauss :l :f1 :f1,

to strauss :l :f1 :f2
blume3 :l :f1
rt 60 
blume3 :l :f2
end

und geben wir strauss 50 blau pink im Eingabefeld ein.

Mit einem Programm können wir verschiedene Sträusse zeichnen, abhängig von der Sechseckgrösse und den Blumenfarben. Durch Eingabe von strauss 20 cyan orange erhalten wir zum Beispiel:

Challenge 3 - Virenbekämpfung

Nachdem wir die letzten Wochen dem Corona-Virus ausgesetzt waren, ja gar die Schulen deswegen geschlossen werden mussten, wollen wir nun aktiv etwas dagegen machen. Genau: Wir programmieren einen Antvirus, der dem ganzen Spuk ein Ende machen soll. Wir wollen zuerst das Virus programmieren und anschliessend einen Antivirus dafür entwickeln.

• Schritt 1 : Virus programmieren

Ein Element, welches in allen Viren enthalten ist, ist das Quadrat. Die Quadrate sind allerdings nicht immer gleich gross... Wir schreiben dazu also ein neues Programm, bei welchem wir mittels Parameter entscheiden können, wie gross die Seitenlänge sein soll:

to quadrat :groesse
repeat 4 [fd :groesse rt 90]
end

Als nächstes wollen wir einen Fühler zeichnen (also eine Linie bestimmter Länge, an deren Ende ein Quadrat ist). Aus der Skizze der Aufgabenstellung entnehmen wir, dass die Länge der Linie jeweils doppelt so gross ist wie die Seitenlänge des darauf sitzenden Quadrats. Wir schreiben also einen parametrisierten Befehl fuehler, bei welchem wir angeben können, wie gross das darauf sitzende Quadrat sein soll (wir nennen diesen Parameter ebenfalls :groesse). Dazu bewegen wir die Schildkröte zunächst um 2*:groesse Schritte nach vorne, um die Linie zu zeichnen. (Wenn das Quadrat also die Seitenlänge 100 hat, so ist die Linie 200 Schritte lang - hat das Quadrat hingegen nur eine Seitenlänge von 80, so ist die Linie nur 160 Schritte lang). Anschliessend wollen wir zur Ausgangsposition des Quadrats laufen. Diese befindet sich in der linken unteren Ecke. Das heisst, dass wir die Schildkröte zunächst um :groesse/2 Schritte nach links bewegen müssen. Erst dann können wir das Quadrat der Grösse :groesse zeichnen und anschliessend das ganze Programm wieder zum Start zurückverfolgen:

to fuehler :groesse
fd :groesse*2 
lt 90 fd :groesse/2 rt 90 
quadrat :groesse
lt 90 bk :groesse/2 rt 90
bk :groesse*2
end

Damit gelingt es uns nun Fühler aller möglichen Grössen zu zeichnen mit zur einem Programm:

Nun wollen wir mehrere solche Fühler zu einem Virus zusammensetzen können. Die Anzahl der Fühler unterscheidet sich von Virus zu Virus, daher wollen wir dazu einen Parameter verwenden. Wir können zwar nicht wissen, welchen Wert der Platzhalter :anzahl am Schluss enthalten wird, welcher die Anzahl der Fühler beschreibt; wir wissen allerdings, dass alle Fühler regelmässig im Kreis verteilt sind. Das heisst, dass die Schildkröte eine ganze Umdrehung (360 Grad) in :anzahl Stopps unterteilen muss und sich demzufolge bei jedem Stopp um genau denselben Winkel (360/:anzahl) drehen muss:

to virus :groesse :anzahl
repeat :anzahl [fuehler :groesse rt 360/:anzahl]
end

Beachte: Obwohl der Parameter :groesse eigentlich nur im Programm fuehler verwendet wird, müssen wir auch dem Programm virus einen Parameter :groesse geben, sodass wir fähig sind, das Programm fuehler anschliessend in virus aufzurufen.

Damit sind wir nun in der Lage, alle möglichen Viren jedweder Grösse und Fühleranzahl zu zeichnen.

• Schritt 2 : Antivirus programmieren

Nun, da der Virus bereits gezeichnet werden kann, machen wir uns besser schnell daran, einen Antivirus dafür zu finden, nicht? 😉

Grundsätzlich haben wir die wichtigsten Teile bereits geschrieben: Wir haben ein Programm, um ein Virus zu zeichnen und wir haben ein Programm, um Quadrate beliebiger Grösse zu zeichnen... Lass uns also um jedes zuvor gezeichnete Quadrat ein weiteres Quadrat zeichnen! Aus der Aufgabenstellung entnehmen wir, dass die gelbe Schutzhülle auf jeder Seite jeweils 50 Schritte grösser ist als das ursprüngliche Quadrat. Das heisst, dass es links und rechts sowie oben und unten jeweils eine Lücke von 25 Schritten gibt:

Um zum Startpunkt des gelben Quadrats zu kommen, geht die Schildkröte also nicht 2*:groesse Schritte nach vorne so wie zuvor beim schwarzen Quadrat, sondern 25 Schritte weniger. Anstatt :groesse/2 Schritte nach links zu laufen wie zuvor beim schwarzen Quadrat, sind es hier 25 Schritte mehr. Zuletzt hat das Quadrat nun nicht die Seitenlänge :groesse wie zuvor, sondern 50 Schritte mehr. Wir schreiben ein Programm antifuehler, welches denselben Effekt hat wie zuvor der Fühler, jedoch nun angepasst auf die Grösse des Antivirus:

to antifuehler :groesse
fd (:groesse*2)-25
lt 90 fd (:groesse/2)+25 rt 90 
quadrat :groesse+50
lt 90 bk (:groesse/2)+25 rt 90
bk :groesse*2-25
end

Wir wenden dieselbe Strategie an wie zuvor beim Virus und schreiben ein Programm antivirus, welches als Parameter die Anzahl der Fühler erhält:

to antivirus :groesse :anzahl
setpc yellow
repeat :anzahl [antifuehler :groesse rt 360/:anzahl]
end

Damit können wir beliebige Schutzhüllen zeichnen, wie beispielsweise hier für virus 100 4, welches wir zuvor gesehen haben:

Alles, was jetzt noch fehlt, ist die Kombination von antivirus und virus. Dies gelingt uns einfach, indem wir direkt nach dem Zeichnen des Antivirus den Virus in die vorbereitete Schutzhülle packen:

to antivirus :groesse :anzahl
setpc yellow
repeat :anzahl [antifuehler :groesse rt 360/:anzahl]
setpc black
repeat :anzahl [fuehler :groesse rt 360/:anzahl]
end

oder mit unserem Programm virus:

to antivirus :groesse :anzahl
setpc yellow
repeat :anzahl [antifuehler :groesse rt 360/:anzahl]
setpc black
virus :groesse :anzahl
end

Beiträge von euch

Hier präsentieren wir ein paar ausgewählte Beiträge, die uns per E-Mail erreicht haben:

Vielen Dank für eure Teilnahme und das Einsenden eurer tollen Lösungen!

Abschluss

Bravo - Gut gemacht!

Du hast das Ende unserer Challenges erreicht, Gratulation! Haben dir unsere Aufgaben gefallen? Gib uns ein Feedback und fülle unsere Umfrage aus (opens new window).

Vielen Dank!